浙江省部分学校2024年中考适应性考试一模数学试卷

更新时间：2024-05-30 浏览次数：136 类型：中考模拟

一、选择题（本大题有10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024七上·凉州期中) $\text{[math]}$ 的相反数是（）

A . 2024 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·河北模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·浙江模拟) 经核算和评价认证，杭州亚运会和亚残运会共排放温室气体882900吨，在亚运会、亚残运会历史上首次实现碳中和，其中数据882900用科学记数法表示是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·浙江模拟) 小浙计划周末在“嘉兴南湖”“丽水浙西南革命根据地纪念馆”“宁波四明山抗日根据地旧址群”三个地点中随机选择一个地点研学．他选中“嘉兴南湖”的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024·浙江模拟) 由4个大小相同的小正方体拼成的几何体如图所示，则其三视图中两种视图完全一样的是（）

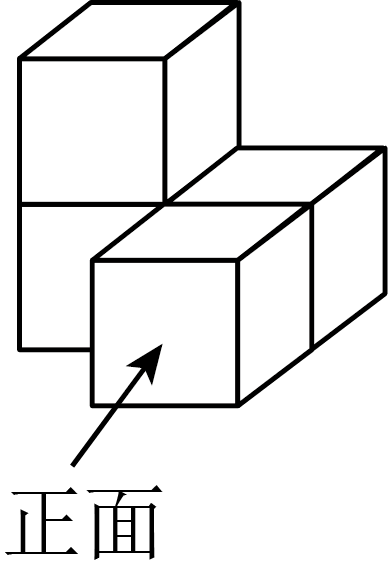
A . 主视图和俯视图 B . 左视图和俯视图 C . 主视图和左视图 D . 以上都不正确

答案解析收藏纠错 + 选题
6. (2024九下·内蒙古自治区模拟) 某篮球队5名场上队员的身高（单位：cm）是：168，184，187，188，197．现用一名身高为178cm的队员换下场上身高为197cm的队员，与换人前相比，场上队员的身高（）

A . 平均数变小，方差变小 B . 平均数变小，方差变大 C . 平均数变大，方差变小 D . 平均数变大，方差变大

答案解析收藏纠错 + 选题
7. (2024九下·连山模拟) 下列选项中，可以用来证明命题“两个无理数的乘积一定是无理数”是假命题的反例是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·浙江模拟) 若 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·浙江模拟) 有一块半径为8米，圆心角为45°的扇形空地需要美化，某同学的设计图如图所示，在扇形空地上修建一个正方形水池，正方形的一条边 $\text{[math]}$ 在边 $\text{[math]}$ 上，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，其他部分种上花圃，已知花圃的面积为16平方米，设 $\text{[math]}$ 的长为 $\text{[math]}$ 米，可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·河北模拟) 已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 均在抛物线 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，点 $\text{[math]}$ 和 $\text{[math]}$ 也在此抛物线上，则下列说法正确的是（）

A . 若 $\text{[math]}$ 恒成立，则 $\text{[math]}$ B . 若 $\text{[math]}$ 恒成立，则 $\text{[math]}$ C . 若 $\text{[math]}$ 恒成立，则 $\text{[math]}$ D . 若 $\text{[math]}$ 恒成立，则 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题有6小题，每小题4分，共24分）

11. (2024八下·浏阳期中) 要使二次根式 $\text{[math]}$ 有意义，实数x的取值范围是

答案解析收藏纠错 + 选题
12. (2024八下·龙泉驿期末) 因式分解： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024九下·浙江模拟) 圆锥的底面半径为 $\text{[math]}$ ，侧面积为 $\text{[math]}$ ，则该圆锥的母线长为．

答案解析收藏纠错 + 选题
14. (2024·浙江模拟) 如图，已知 $\text{[math]}$ ，直线 $\text{[math]}$ 分别与 $\text{[math]}$ ， $\text{[math]}$ 相交于 $\text{[math]}$ ， $\text{[math]}$ 两点，把一块含 $\text{[math]}$ 角的三角尺按如图所示的位置摆放，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
15. (2024·浙江模拟) 如图， $\text{[math]}$ 平行于 $\text{[math]}$ 轴，点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上，点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上， $\text{[math]}$ ，若四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2024·浙江模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，点 $\text{[math]}$ ， $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到点 $\text{[math]}$ ， $\text{[math]}$ ，若在运动过程中 $\text{[math]}$ 的度数最大值恰好为 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题

三、解答题（本大题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分．解答应写出文字说明、证明过程或演算步骤）

17. (2024九下·浙江模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024八上·宝安开学考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024·浙江模拟) 如图，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 是对角线 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 的直线分别交边 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）作 $\text{[math]}$ 的平分线交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形．
答案解析收藏纠错 + 选题
20. (2024·浙江模拟) 某中学为了解本校九年级男生1000米跑的成绩，从九年级240名男生中随机抽取了部分男生进行测试，并把测试成绩进行统计，绘制成如下图表（每小组成绩包含最小值，不包含最大值）．
九年级若干名男生1000米跑成绩的频数分布表
组别（秒）
频数
频数
$\text{[math]}$
1
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
8
$\text{[math]}$
$\text{[math]}$
5
$\text{[math]}$
$\text{[math]}$
2
$\text{[math]}$
合计
$\text{[math]}$
1
请根据上面的图表，回答下列问题：
1. （1） $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）补全频数分布直方图；
3. （3）若男生1000米跑在 $\text{[math]}$ 秒以内的同学为优秀，请你估计该校九年级240名男生中1000米跑的成绩优秀的人数．
答案解析收藏纠错 + 选题

21. (2024·浙江模拟) 根据以下素材，探索完成任务：

测算雷锋塔的高度
素材1	如图1，雷峰塔前有一斜坡 $\text{[math]}$ ，长为10米，坡度为 $\text{[math]}$ ，高为 $\text{[math]}$
素材2	利用测角仪在斜坡底的点 $\text{[math]}$ 处测得塔尖点 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，在斜坡顶的点 $\text{[math]}$ 处测得塔尖点 $\text{[math]}$ 的仰角为 $\text{[math]}$ （其中点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一直线上，如图2）
素材3	查阅锐角三角函数表	$\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
任务1	获取数据	计算斜坡的高度 $\text{[math]}$
任务2	分析计算	通过观察，计算雷峰塔的高度（结果保留整数）

答案解析收藏纠错 + 选题

22. (2024·浙江模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ 两地相距 $\text{[math]}$ ，甲、乙两人沿同一条公路从 $\text{[math]}$ 地出发到 $\text{[math]}$ 地，乙骑自行车，甲骑摩托车．图中 $\text{[math]}$ 、折线 $\text{[math]}$ 分别表示甲、乙离开 $\text{[math]}$ 地的路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的函数关系的图象，根据图象填空：
1. （1）甲、乙两人相遇前乙的速度为，相遇后乙的速度为；
2. （2）求甲离开 $\text{[math]}$ 地的路程 $\text{[math]}$ 与时间 $\text{[math]}$ 的函数表达式；
3. （3）若甲、乙两人之间的距离表示为 $\text{[math]}$ ，请在图2中画出距离 $\text{[math]}$ 与时间 $\text{[math]}$ 的函数关系图象．
答案解析收藏纠错 + 选题
23. (2024·浙江模拟)
1. （1）【基础巩固】如图1，已知 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；
2. （2）【尝试应用】如图2，已知 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ 和 $\text{[math]}$ 上， $\text{[math]}$ 是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）【拓展提高】如图3，已知 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别在直线 $\text{[math]}$ 和直线 $\text{[math]}$ 上， $\text{[math]}$ 是边 $\text{[math]}$ 上一点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的两条直角边长之比为 $\text{[math]}$ ，直接写出此时 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
24. (2024·浙江模拟) 如图， $\text{[math]}$ 内接于圆 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的高线， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是等腰三角形；
2. （2）求证： $\text{[math]}$ ；
3. （3）若点 $\text{[math]}$ 是 $\text{[math]}$ 上一动点， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．
  ①若 $\text{[math]}$ 与 $\text{[math]}$ 相似，求 $\text{[math]}$ 的长；
  ②当 $\text{[math]}$ 的面积与 $\text{[math]}$ 的面积差最大时，直接写出此时 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省部分学校2024年中考适应性考试一模数学试卷

副标题：

*注意事项：

浙江省部分学校2024年中考适应性考试一模数学试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

组别（秒）	频数	频数
$\text{[math]}$	1	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	8	$\text{[math]}$
$\text{[math]}$	5	$\text{[math]}$
$\text{[math]}$	2	$\text{[math]}$
合计	$\text{[math]}$	1