广东省东莞外国语学校2023-2024学年高一（下）第一次段...

更新时间：2024-07-31 浏览次数：11 类型：月考试卷

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1. (2024高一下·东莞月考) $\text{[math]}$ 是虚数单位，若 $\text{[math]}$ 为纯虚数，则实数 $\text{[math]}$ 的值为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·东莞月考) 下列命题正确的是( )

A . 有两个面平行，其余各面都是四边形的几何体是棱柱 B . 有一个面是多边形，其余各面是三角形的几何体是棱锥 C . 有两个面平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行的几何体是棱柱 D . 用一个平面去截棱锥，底面与截面之间的部分组成的几何体是棱台

答案解析收藏纠错 + 选题
3. (2024高一下·东莞月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高一下·东莞月考) 如图，正方形 $\text{[math]}$ 的边长为 $\text{[math]}$ ，它是水平放置的一个平面图形的直观图，则原图的周长是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·东莞月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则向量 $\text{[math]}$ 在向量 $\text{[math]}$ 上的投影向量为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一下·东莞月考) 若虚数单位 $\text{[math]}$ 是关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·韶关月考) 在 $\text{[math]}$ 中， $\text{[math]}$ 是边 $\text{[math]}$ 上一点，且 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，记 $\text{[math]}$ ，则 $\text{[math]}$ ( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高一下·韶关期中) 费马点是指位于三角形内且到三角形三个顶点距离之和最小的点 $\text{[math]}$ 当三角形三个内角都小于 $\text{[math]}$ 时，费马点与三角形三个顶点的连线构成的三个角都为 $\text{[math]}$ 已知在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的费马点，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的取值范围是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。

9. (2024高一下·东莞月考) 已知 $\text{[math]}$ ，则下列说法正确的是( )

A . $\text{[math]}$ 的最小值为 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，与 $\text{[math]}$ 垂直的单位向量只能为 $\text{[math]}$ D . 若向量 $\text{[math]}$ 与向量 $\text{[math]}$ 的夹角为钝角，则 $\text{[math]}$ 的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一下·东莞月考) 已知复数 $\text{[math]}$ ， $\text{[math]}$ ，下列说法正确的是( )

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ D . 若复数 $\text{[math]}$ ， $\text{[math]}$ 不相等且 $\text{[math]}$ ，则 $\text{[math]}$ 在复平面内对应的点在一条直线上

答案解析收藏纠错 + 选题
11. (2024高一下·东莞月考) 在 $\text{[math]}$ 中，内角A，B，C所对的边分别为a，b，c，且 $\text{[math]}$ ，则下列选项正确的是（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ 有两解 B . 若 $\text{[math]}$ ，则 $\text{[math]}$ 无解 C . 若 $\text{[math]}$ 为锐角三角形，且 $\text{[math]}$ ，则 $\text{[math]}$ D . 若 $\text{[math]}$ ，则 $\text{[math]}$ 的最大值为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分。

12. (2024高一下·东莞月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024高一下·东莞月考) 设 $\text{[math]}$ 是不共线的两个向量， $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点共线，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
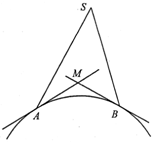
14. (2024高一下·东莞月考) $\text{[math]}$ 世纪阿拉伯天文学家阿尔库希设计出一种方案，通过两个观察者异地同时观测同一颗小天体来测定小天体的高度．如图，有两个观察者在地球上 $\text{[math]}$ ， $\text{[math]}$ 两地同时观测到一颗卫星 $\text{[math]}$ ，仰角分别为 $\text{[math]}$ 和 $\text{[math]}$ 表示当地的水平线，即为地球表面的切线 $\text{[math]}$ ，设地球半径为 $\text{[math]}$ ，弧 $\text{[math]}$ 的长度为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则卫星 $\text{[math]}$ 到地面的高度为．

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。

15. (2024高一下·东莞月考) 已知复数 $\text{[math]}$ ．
1. （1）若复数 $\text{[math]}$ 为实数，求 $\text{[math]}$ ；
2. （2）若复数对应点在第二象限，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
16. (2024高一下·东莞月考) 设 $\text{[math]}$ 的内角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边分别为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的周长．
答案解析收藏纠错 + 选题
17. (2024高一下·东莞月考) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）设实数 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
2. （2）若以线段 $\text{[math]}$ ， $\text{[math]}$ 为邻边作平行四边形 $\text{[math]}$ ，求向量 $\text{[math]}$ 与 $\text{[math]}$ 所夹角的余弦值．
答案解析收藏纠错 + 选题
18. (2024高一下·东莞月考) 在 $\text{[math]}$ 中，角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所对的边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且满足 $\text{[math]}$
1. （1）求角 $\text{[math]}$ 的大小；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2024高一下·东莞月考) 如图， $\text{[math]}$ ， $\text{[math]}$ 是单位圆 $\text{[math]}$ 圆心为 $\text{[math]}$ 上两动点， $\text{[math]}$ 是劣弧 $\text{[math]}$ 含端点 $\text{[math]}$ 上的动点 $\text{[math]}$ 记 $\text{[math]}$ 均为实数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 时，当点 $\text{[math]}$ 恰好运动到劣弧 $\text{[math]}$ 的中点时，求 $\text{[math]}$ 的值．
2. （2）若 $\text{[math]}$ 时，求 $\text{[math]}$ 的取值范围；
3. （3）若 $\text{[math]}$ ，记向量 $\text{[math]}$ 和向量 $\text{[math]}$ 的夹角为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值．
答案解析收藏纠错 + 选题