河北省石家庄市平山县2023-2024学年七年级下学期月考数...

更新时间：2024-07-25 浏览次数：14 类型：月考试卷

一、选择题（本大题共14个小题，共38分，1~10小题每小题3分，11~14小题各2分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024七下·平山月考) 有理数8的立方根是（）

A . 2 B . －2 C . 4 D . ±2

答案解析收藏纠错 + 选题
2. (2024七下·平山月考) 如图，将一张长方形纸对折两次，产生的折痕与折痕之间的位置关系是（）

A . 平行 B . 垂直 C . 平行或垂直 D . 无法确定

答案解析收藏纠错 + 选题
3. (2024七下·厦门期中) 用符号表示“4的平方根是±2”，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·平山月考) 如图，与∠1是同旁内角的是（）

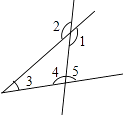
A . ∠2 B . ∠3 C . ∠4 D . ∠5

答案解析收藏纠错 + 选题
5. (2024七下·平山月考) 化简 $\text{[math]}$ 的值是（）

A . 2 B . 3 C . ±2 D . ±3

答案解析收藏纠错 + 选题
6. (2023八上·余姚竞赛) 能说明命题“一个钝角与一个锐角的差一定是锐角”是假命题的反例是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·平山月考) 若 $\text{[math]}$ ， $\text{[math]}$ ，则x的值是（）

A . 0.5981 B . ±0.5981 C . 0.214 D . ±0.214

答案解析收藏纠错 + 选题
8. (2024七下·平山月考) 如图是佳佳同学在体育课上立定跳远测试留下的脚印，则她的跳远成绩为（）．

A . 2.35米 B . 2.11米 C . 2.05米 D . 2.20米

答案解析收藏纠错 + 选题
9. (2024七下·金安期中) 已知 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的值（）

A . 86.2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·平山月考) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ，所以点O、M、N三点共线的理由（）

A . 三点确定一条直线 B . 如果两条直线都与第三条直线平行，那么这两条直线重合 C . 经过直线外一点，有且只有一条直线与这条直线平行 D . 过三点可作一条直线与已知直线平行

答案解析收藏纠错 + 选题
11. (2024七下·平山月考) 若m＋4与m－2是同一个正数的两个不同平方根，则m的值为（）

A . －3 B . －1 C . 1 D . 3

答案解析收藏纠错 + 选题
12. (2024七下·平山月考) 下列图形中，线段AD的长度表示点A到直线BC距离的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
13. (2024七下·平山月考) 整数a满足 $\text{[math]}$ ，则a的值为（）

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
14. (2024七下·平山月考) 如图，△ABC沿射线BC方向平移到△DEF（点E在线段BC上）．若BF＝10cm，EC＝4cm，则平移距离为（）

A . 3cm B . 4cm C . 6cm D . 10cm

答案解析收藏纠错 + 选题

二、填空题（本大题共3个小题，共10分．15小题2分，16~17小题各4分，每空2分）

15. (2024七下·平山月考) 命题“同位角相等”的题设是．

答案解析收藏纠错 + 选题
16. (2024七下·平山月考) 如图是一种对顶角量角器，它所测量的角的度数是°，用它测量角的原理是．

答案解析收藏纠错 + 选题
17. (2024七下·平山月考) 有一个数值转换器，原理如图．
⑴当输入的x为16时，输出的y＝．
⑵若始终输不出y值、则输入的x＝．

答案解析收藏纠错 + 选题

三、解答题（本大题共七个小题，满分72分，解答题应写出必要的解题步骤或文字说明）

18. (2024七下·平山月考) 如图，已知三角形ABC及一点E ，平移三角形ABC、使点C移动到点E ，请画出平移后的三角形DFE ．并保留画图痕迹．

答案解析收藏纠错 + 选题
19. (2024七下·平山月考) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2024七下·平山月考) 如图，直线AB和直线CD相交于点O ， OB平分∠EOD ．
1. （1）图中∠AOC的对顶角是，邻补角是；
2. （2）若∠AOC＝35°，求∠EOC的度数．
答案解析收藏纠错 + 选题
21. (2024七下·平山月考) 图1是由10个边长均为1的小正方形组成的图形，我们沿图中虚线AB ， BC将它剪开后，重新拼成一个大正方形ABCD ．
1. （1）在图1中，拼成的大正方形ABCD的面积为，边AD的长为；
2. （2） 知识运用：
  现将图1水平放置在如图2所示的数轴上，使得大正方形的顶点B与数轴上表示－1的点重合，若以点B为圆心，BC边的长为半径画圆，与数轴交于点E ，求点E表示的数．
答案解析收藏纠错 + 选题
22. (2024七下·平山月考) 某市在招商引资期间，把已倒闭的油泵厂出租给外地某投资商，该投资商为减少固定资产投资，将原来400m²的正方形场地改建成315m²的长方形场地，且其长、宽的比为5：3．
1. （1）求原来正方形场地的周长；
2. （2）如果把原来正方形场地的铁栅栏围墙全部利用，围成新场地的长方形围墙，那么这些铁栅栏是否够用？试利用所学知识说明理由．
答案解析收藏纠错 + 选题
23. (2024七下·南康期中) 如图是一种躺椅及其结构示意图，扶手AB与底座CD都平行于地面EF ，前支架OE与后支架OF分别与CD交于点G和点D ， AB与DM交于点N ， ∠AOE＝∠BNM ．
1. （1）请对 $\text{[math]}$ 说明理由；
2. （2）若OE平分∠AOF ， ∠ODC＝30°，求扶手AB与靠背DM的夹角∠ANM的度数．
答案解析收藏纠错 + 选题
24. (2024七下·平山月考) 【学科融合】如图1，在反射现象中，反射光线，入射光线和法线都在同一个平面内；反射光线和入射光线分别位于法线两侧；反射角r等于入射角i ．这就是光的反射定律．
1. （1）学完光的反射定律，数学兴趣小组的同学想利用这个定律结合数学知识制作一个简易潜望镜，并画出了潜望镜的工作原理示意图，如图2所示，AB、CD是平行放置的两面平面镜，已知光线经过平面镜反射时、有∠2＝∠1，∠4＝∠3，请问进入潜望镜的光线EF和离开潜望镜的光线GH是否平行，说明理由．
2. （2） 【尝试探究】
  把两个平面镜AB ， BC按图3所示位置放置， $\text{[math]}$ ，光线经过两次反射后，∠2＝∠1，∠4＝∠3，反射光线GH与入射光线EF平行但方向相反、求 $\text{[math]}$ 的度数．【注：三角形的三个角的和是180°】
答案解析收藏纠错 + 选题