浙江省杭州市浙里特色联盟2023-2024学年高一下学期4月...

更新时间：2024-05-17 浏览次数：13 类型：期中考试

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1. (2024高一下·杭州期中) 集合 $\text{[math]}$ ，集合 $\text{[math]}$ ，则集合 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·杭州期中) 已知 $\text{[math]}$ 是虚数单位，则复数 $\text{[math]}$ 在复平面内所对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024高一下·杭州期中) 设 $\text{[math]}$ 是三个不同平面，且 $\text{[math]}$ ， $\text{[math]}$ ，则“ $\text{[math]}$ ”是“ $\text{[math]}$ ”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
4. (2024高一下·杭州期中) 若命题 $\text{[math]}$ ，有 $\text{[math]}$ 且 $\text{[math]}$ ，则命题 $\text{[math]}$ 为（）

A . $\text{[math]}$ 且 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·杭州期中) 已知向量 $\text{[math]}$ ，满足 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一下·杭州期中) 已知函数 $\text{[math]}$ ，则下列说法正确的是（）

A . $\text{[math]}$ 的周期为 $\text{[math]}$ B . $\text{[math]}$ 的图象关于直线 $\text{[math]}$ 对称 C . $\text{[math]}$ 是 $\text{[math]}$ 的一个对称中心 D . $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增

答案解析收藏纠错 + 选题
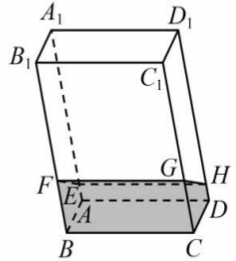
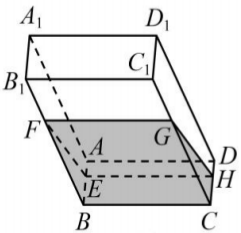
7. (2024高一下·杭州期中) 如图，透明塑料制成的长方体容器 $\text{[math]}$ 内灌进一些水，固定容器底面一边 $\text{[math]}$ 于地面上，再将容器绕边 $\text{[math]}$ 倾斜．随着倾斜度的不同，在下面四个命题中错误的是（）
1. （1）（2）（3）
  
  A . 没有水的部分始终呈棱柱形 B . 棱 $\text{[math]}$ 始终与水面所在平面平行 C . 水面 $\text{[math]}$ 所在四边形的面积为定值 D . 当容器倾斜如图（3）所示时， $\text{[math]}$ 是定值
答案解析收藏纠错 + 选题
8. 已知 $\text{[math]}$ 的内角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 面积的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对得6分，部分选对的得部分分，有选错的得0分。

9. (2024高一下·杭州期中) 已知复数 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的共轭复数，则（）

A . $\text{[math]}$ B . $\text{[math]}$ 的虚部是 $\text{[math]}$ C . $\text{[math]}$ 在复平面内对应的点位于第二象限 D . 复数 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个根

答案解析收藏纠错 + 选题
10. (2024高一下·杭州期中) 已知非零向量 $\text{[math]}$ ，以下命题正确的有（）

A . 若 $\text{[math]}$ ，则 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 若 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为锐角 D . 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024高一下·杭州期中) 如图，棱长为2的正方体 $\text{[math]}$ 中， $\text{[math]}$ 为棱 $\text{[math]}$ 的中点， $\text{[math]}$ 为正方形 $\text{[math]}$ 内一个动点（包括边界），且 $\text{[math]}$ 平面 $\text{[math]}$ ，则下列说法正确的有（）

A . 记 $\text{[math]}$ 的中点为 $\text{[math]}$ ， $\text{[math]}$ 上存在一点 $\text{[math]}$ ，使得面 $\text{[math]}$ 面 $\text{[math]}$ B . 动点 $\text{[math]}$ 轨迹的长度为 $\text{[math]}$ C . 三棱锥 $\text{[math]}$ 体积的最小值为 $\text{[math]}$ D . 当三棱锥 $\text{[math]}$ 的体积最大时，其外接球的表面积为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分．

12. (2024高一下·杭州期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024高一下·杭州期中) 已知圆锥的底面圆周在球 $\text{[math]}$ 的球面上，顶点为球心 $\text{[math]}$ ，圆锥的高为3，且圆锥的侧面展开图是一个半圆，则球 $\text{[math]}$ 的表面积为．

答案解析收藏纠错 + 选题
14. (2024高一下·杭州期中) 如图所示，为了测量某座山的山顶 $\text{[math]}$ 到山脚某处 $\text{[math]}$ 的距离（ $\text{[math]}$ 垂直于水平面），研究人员在距 $\text{[math]}$ 研究所 $\text{[math]}$ 处的观测点 $\text{[math]}$ 处测得山顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，山脚 $\text{[math]}$ 的俯角为 $\text{[math]}$ ．若该研究员还测得 $\text{[math]}$ 到 $\text{[math]}$ 处的距离比到 $\text{[math]}$ 处的距离多 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。

15. (2024高一下·杭州期中) 已知复数 $\text{[math]}$ ， $\text{[math]}$ 为虚数单位．
1. （1）求 $\text{[math]}$ ；
2. （2）若复数 $\text{[math]}$ 是关于 $\text{[math]}$ 的方程 $\text{[math]}$ 的一个根，求实数 $\text{[math]}$ 的值；
3. （3）若复数 $\text{[math]}$ 满足 $\text{[math]}$ ，求 $\text{[math]}$ 的最值．
答案解析收藏纠错 + 选题
16. (2024高一下·杭州期中) 在 $\text{[math]}$ 中，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的模；
2. （2）求向量 $\text{[math]}$ 与 $\text{[math]}$ 夹角的余弦值；
3. （3）若点 $\text{[math]}$ 在边 $\text{[math]}$ 上，求 $\text{[math]}$ 的范围．
答案解析收藏纠错 + 选题
17. (2024高一下·杭州期中) 三棱柱 $\text{[math]}$ 的棱长都为2， $\text{[math]}$ 和 $\text{[math]}$ 分别是 $\text{[math]}$ 和 $\text{[math]}$ 的中点．
1. （1）求证：直线 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离为 $\text{[math]}$ ，求三棱锥 $\text{[math]}$ 的体积．
答案解析收藏纠错 + 选题
18. (2024高一下·杭州期中) 在锐角三角形 $\text{[math]}$ 中，角 $\text{[math]}$ 的对边分别为 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求角 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2024高一下·杭州期中) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，
1. （1）求 $\text{[math]}$ 的解析式；
2. （2）关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集为 $\text{[math]}$ ，求实数 $\text{[math]}$ 的取值范围；
3. （3）关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集中的正整数解恰有3个，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题