河北省沧州市泊头市2023-2024学年七年级下学期数学期中...

更新时间：2024-05-14 浏览次数：4 类型：期中考试

一、选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024七下·泊头期中) 下列方程中，属于二元一次方程的是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·泊头期中) 甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，能用其中一部分平移得到的是（　　）

A . 杯 B . 立 C . 比 D . 曲

答案解析收藏纠错 + 选题
3. (2024七下·平城月考) 若 $\text{[math]}$ 是方程 $\text{[math]}$ 的一个解，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·泊头期中) 下列各式中，与 $\text{[math]}$ 运算结果相同的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·泊头期中) 在显微镜下，人体的一种细胞形状可以近似地看成圆形，它的半径约为 $\text{[math]}$ 米，用科学记数法表示为 $\text{[math]}$ ，则n的值为（）

A . 7 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
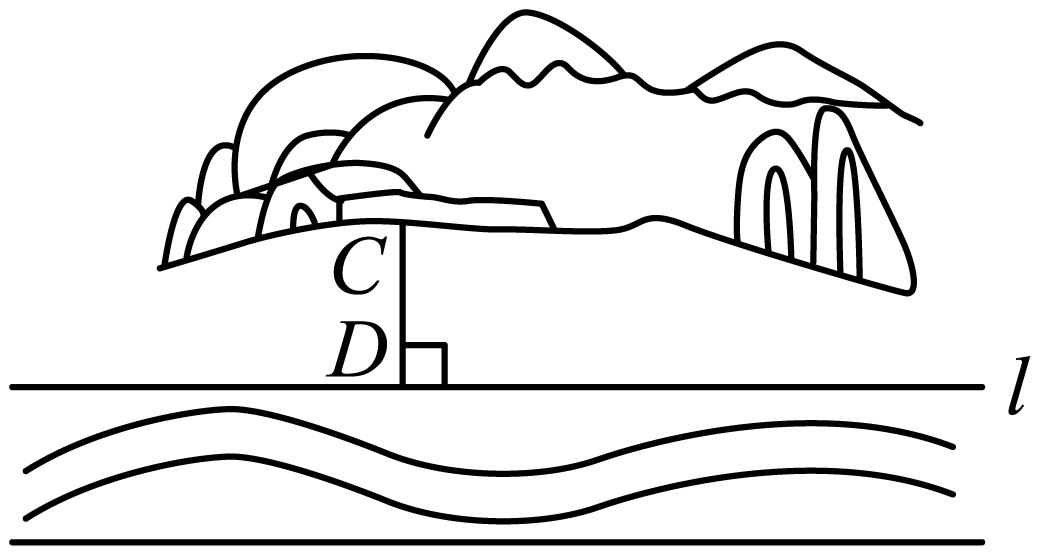
6. (2024七下·泊头期中) 如图，某村庄要在河岸 $\text{[math]}$ 上建一个水泵房引水到 $\text{[math]}$ 处．他们的做法是：过点 $\text{[math]}$ 作 $\text{[math]}$ 于点D，将水泵房建在了D处，这样做最节省水管长度，其数学道理是（）

A . 两点确定一条直线 B . 垂线段最短 C . 两点之间，线段最短 D . 过一点有且仅有一条直线与已知直线垂直

答案解析收藏纠错 + 选题
7. (2024七下·永善期中) 老师在黑板上画出如图所示的图形，要求学生添加条件，使得AB∥CD ，随后抽取了四名学生的答案纸展示如下：
甲：∠B+∠BCD＝180°；
乙：∠1＝∠2；
丙：∠B＝∠DCE；
丁：∠3＝∠4．
则不能得到AB∥CD的是（　　）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
8. (2024七下·泊头期中) 某农场去年计划生产玉米和小麦共 $\text{[math]}$ 吨，采用新技术后，实际产量为 $\text{[math]}$ 吨，其中玉米超产 $\text{[math]}$ ，小麦超产 $\text{[math]}$ ，设该农场去年计划生产玉米 $\text{[math]}$ 吨、小麦 $\text{[math]}$ 吨，则所列方程组正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024七下·泊头期中) 图1是古人利用光的反射定律改变光路的方法，即（如图2）反射光线与入射光线、法线在同一平面上，法线垂直于平面镜，反射光线和入射光线位于法线的两侧，反射角等于入射角．如图3，小轩的乒乓球掉到沙发下，他借助平面镜，利用光的反射原理找到了乒乓球的位置，已知法线 $\text{[math]}$ ，反射光线 $\text{[math]}$ 与水平线的夹角 $\text{[math]}$ ，则平面镜 $\text{[math]}$ 与水平线 $\text{[math]}$ 的夹角 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·泊头期中) 下列命题中真命题的个数有（）
①经过已知直线外一点，有且只有一条直线与已知直线平行；
②垂直于同一条直线的两条直线平行；
③两条直线被第三条直线所截，同旁内角互补；
④平行于同一条直线的两条直线平行；
⑤一个角的两边与另一个角的两边分别平行，则这两个角相等．

A . $\text{[math]}$ 个 B . $\text{[math]}$ 个 C . $\text{[math]}$ 个 D . $\text{[math]}$ 个

答案解析收藏纠错 + 选题
11. (2024八上·长沙开学考) 若关于x ， y的二元一次方程组 $\text{[math]}$ 的解满足 $\text{[math]}$ ，则k的值为（　　）

A . 0 B . 1 C . 2 D . -1

答案解析收藏纠错 + 选题
12. (2024七下·泊头期中) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共4个小题，每小题3分，共12分）

13. (2024七下·泊头期中) 已知二元一次方程 $\text{[math]}$ ，用含 $\text{[math]}$ 代数式表示 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024七下·泊头期中) 若 $\text{[math]}$ 与 $\text{[math]}$ 的乘积中不含 $\text{[math]}$ 的一次项，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2024七下·泊头期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024七下·泊头期中) 如图，直线 $\text{[math]}$ 上有两点 A、C ，分别引两条射线 $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 在直线 $\text{[math]}$ 异侧．若 $\text{[math]}$ ，射线 $\text{[math]}$ 分别绕 A点，C点以 1 度/秒和 6 度/秒的速度同时顺时针转动，设时间为 t秒，在射线 CD转动一周的时间内，当时间 t的值为时， $\text{[math]}$ 与 $\text{[math]}$ 平行．

答案解析收藏纠错 + 选题

三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）

17. (2024七下·泊头期中) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2024七下·泊头期中) 课堂上老师布置了一道题目：解方程组 $\text{[math]}$ ．
1. （1）小组讨论时，发现有同学这么做：
  解：①＋②，得 $\text{[math]}$ ．解得 $\text{[math]}$ ．
  把 $\text{[math]}$ 代入①，…
  该同学解这个方程组的过程中使用了消元法，目的是把二元一次方程组转化为．
2. （2）请用另一种消元的方法解这个方程组．
答案解析收藏纠错 + 选题
19. (2024七下·泊头期中) 在正方形网格中，每个小正方形的边长均为 $\text{[math]}$ 个单位长度，三角形 $\text{[math]}$ 的三个顶点的位置如图所示．现将三角形 $\text{[math]}$ 沿着点 $\text{[math]}$ 到点 $\text{[math]}$ 的方向平移，使点 $\text{[math]}$ 变换为点 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 的对应点．
1. （1）请画出平移后的三角形 $\text{[math]}$ ；
2. （2）若连接 $\text{[math]}$ ， $\text{[math]}$ ，则这两条线段之间的关系是．
答案解析收藏纠错 + 选题
20. (2024七下·泊头期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024七下·泊头期中) 完成下面推理过程，填空并在括号内写明依据．
已知：如图 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．
证明：∵ $\text{[math]}$ （已知）
∴ $\text{[math]}$     ▲    （                  ）
∴ $\text{[math]}$ （                  ）
∵ $\text{[math]}$ （已知）
∴ $\text{[math]}$ （等量代换）
∴ $\text{[math]}$     ▲    （                  ）
∴ $\text{[math]}$     ▲    （                  ）
又∵ $\text{[math]}$ （已知）
∴ $\text{[math]}$
∴ $\text{[math]}$ （                  ）

答案解析收藏纠错 + 选题
22. (2024七下·泊头期中) 为了响应“绿色环保，节能减排”的号召，小明家准备购买A ， B两种型号的节能灯，若购买2只A型3只B型节能灯需要 80元，购买1只A型4只B型节能灯需要65元．
1. （1） A ， B两种型号节能灯的单价分别是多少？
2. （2）要求这两种节能灯都买，恰好用了200元，有哪几种购买方案？
答案解析收藏纠错 + 选题
23. (2024七下·泊头期中) 如图 $\text{[math]}$ ，是一个长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图 $\text{[math]}$ ）．
1. （1）自主探究：如果用两种不同的方法表示图 $\text{[math]}$ 中阴影部分的面积，可以得到一个等量关系：；
2. （2）知识运用：若 $\text{[math]}$ ， $\text{[math]}$ ．则 $\text{[math]}$ ；
3. （3）知识迁移：设 $\text{[math]}$ ， $\text{[math]}$ ，化简 $\text{[math]}$ 的结果为；
4. （4）知识延伸：若 $\text{[math]}$ ，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2024七下·泊头期中) 在综合与实践课上，老师以“两条平行线AB ， CD和一块含 $\text{[math]}$ 角的直角三角尺EFG（ $\text{[math]}$ ， $\text{[math]}$ ）”为主题开展数学活动．
1. （1）如图①，若直角三角尺的 $\text{[math]}$ 角的顶点G放在CD上， $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）如图②，小颖把直角三角尺的两个锐角的顶点E ， G分别放在AB和CD上，请你探索并说明 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；
3. （3）如图③，小亮把直角三角尺的直角顶点F放在CD上， $\text{[math]}$ 角的顶点E放在AB上．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是什么（用含 $\text{[math]}$ ， $\text{[math]}$ 的式子表示）？请说明理由．
答案解析收藏纠错 + 选题