题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川南充市阆中中学校2023-2024学年八年级下学期数学期...

更新时间：2024-05-15 浏览次数：4 类型：期中考试

一、单项选择题（本题共10个小题，每小题4分，共40分）

1. (2024八下·阆中期中) 下列二次根式中属于最简二次根式的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·阆中期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·阆中期中) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是（）

A . $\text{[math]}$ ＜1 B . $\text{[math]}$ ≥1 C . $\text{[math]}$ ≤1 D . $\text{[math]}$ ＞1

答案解析收藏纠错 + 选题
4. (2024八下·阆中期中) 由下列各组线段中，能组成直角三角形的一组是（）

A . 1，2，3 B . 3，4，6 C . $\text{[math]}$ D . 9，12，15

答案解析收藏纠错 + 选题
5. (2024九下·秦安模拟) $\text{[math]}$ 是某三角形三边的长，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 10 D . 4

答案解析收藏纠错 + 选题
6. (2024·澧县模拟)
如图，菱形中，对角线AC、BD交于点O ， E为AD边中点，菱形ABCD的周长为28，则OE的长等于（　　）

A . 3.5 B . 4 C . 7 D . 14

答案解析收藏纠错 + 选题
7. (2024八下·阆中期中) 如图，已知△ABC ， ∠ACB=90°，AB=10，AC=8，D、E分别是AB、AC的中点，连接ED ，则DE的长为（）

A . 4 B . 5 C . 3 D . 3.5

答案解析收藏纠错 + 选题
8. (2024八下·阆中期中) 四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点O ，给出下列四组条件：① $\text{[math]}$ ；② $\text{[math]}$ ， $\text{[math]}$ ；③ $\text{[math]}$ ， $\text{[math]}$ ；④ $\text{[math]}$ ， $\text{[math]}$ ；其中一定能判定这个四边形是平行四边形的条件有（）

A . 4组 B . 3组 C . 2组 D . 1组

答案解析收藏纠错 + 选题
9. (2024八下·阆中期中) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将矩形沿 $\text{[math]}$ 折叠，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，则重叠部分 $\text{[math]}$ 的面积为（）

A . 10 B . 12 C . 16 D . 20

答案解析收藏纠错 + 选题
10. (2024八下·阆中期中) 如图，在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM ， ON分别交AB ， BC于点E ， F ，且∠EOF=90°，BO ， EF交于点P ，则下面结论：
①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；③正方形ABCD的面积等于四边形OEBF面积的4倍；④BE＋BF= $\text{[math]}$ OA ．
其中正确结论的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题(本大题共8个小题，每题4分，共32分)

11. (2024九下·天祝模拟) 计算： $\text{[math]}$ + $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2024九下·天祝模拟) 若 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2024八下·南昌期中) 如图，以直角△ABC的三边为边向外作正方形，其面积分别为S₁、S₂、S₃ ，且S₁<S₂<S₃ ，若S₁＝9，S₃＝25，则S₂为．

答案解析收藏纠错 + 选题
14. (2024九下·凉州模拟) 若直角三角形两边的长分别为a、b且满足 $\text{[math]}$ +|b-4|=0，则第三边的长是。

答案解析收藏纠错 + 选题
15. (2024八下·万州期中) 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2024八下·阆中期中) 如图，在平面直角坐标系中，四边形OABC是菱形．若点A的坐标是（3，4），则菱形的周长为．

答案解析收藏纠错 + 选题
17. (2024八下·阆中期中) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中点．若 $\text{[math]}$ ， $\text{[math]}$ ，则平行四边形 $\text{[math]}$ 的周长是．

答案解析收藏纠错 + 选题
18. (2024八下·阆中期中) 如图，在Rt△ABC中，∠ACB=90°，AC=BC ，点M在AC边上，且AM=1，MC=3，动点P在AB边上，连接PC ， PM ，则PC+PM的最小值是．

答案解析收藏纠错 + 选题

三、解答题(本大题共7个小题，共78分．解答应写出必要的文字说明、证明过程或演算步骤)

19. (2024八下·阳新) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2024八下·阆中期中) 已知： $\text{[math]}$ ， $\text{[math]}$ ，求下列各式值．
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2024八下·阆中期中) 四边形 $\text{[math]}$ 中， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求四边形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
22. (2024八下·阆中期中) 如图，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两点，且 $\text{[math]}$ ．
求证：四边形 $\text{[math]}$ 是平行四边形．

答案解析收藏纠错 + 选题
23. (2024八下·阆中期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，E是 $\text{[math]}$ 的中点，过点A作 $\text{[math]}$ 的平行线交 $\text{[math]}$ 的延长线于点F ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，试判断四边形 $\text{[math]}$ 的形状，并证明你的结论．
答案解析收藏纠错 + 选题
24. (2024八下·阆中期中) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 交于点F ，延长 $\text{[math]}$ 到点C ，使 $\text{[math]}$ ，延长 $\text{[math]}$ 到点D ，使 $\text{[math]}$ ，连接 $\text{[math]}$
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ，求菱形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
25. (2024八下·阆中期中) 如图，在矩形ABCD中， AB=3，AD=4，E是BC上一动点，将△ABE沿AE折叠后得到△AFE ，点F在矩形ABCD内部，延长AF交CD于点G；
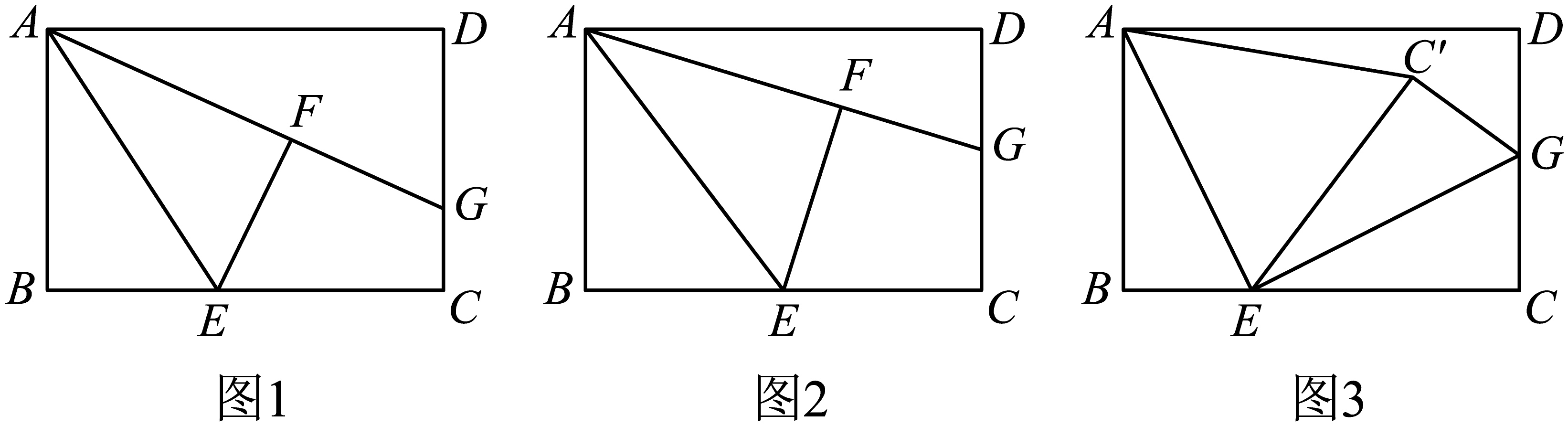
1. （1）如图1，当∠DAG=30° 时，求BE的长；
2. （2）如图2，当点E是BC的中点时，求线段GC的长；
3. （3）如图3，在矩形ABCD中，E ， G分别是BC、CD上的一点，AE $\text{[math]}$ EG ，将△EGC沿EG翻折得 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ 是以AE为腰的等腰三角形，则BE的值为▲ ．（直接写出答案）
答案解析收藏纠错 + 选题

试卷信息