江西省吉安市2023-2024学年九年级下学期数学期中试题

更新时间：2024-05-31 浏览次数：4 类型：期中考试

一、选择题（本大题共6小题，每小题3分，共18分）

1. (2024九下·吉安期中) 下列各数中，是负数的是（）

A . 5 B . $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·吉安期中) 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·吉安期中) 在长春市“暖房子工程”实施过程中，某工程队做了面积为632000的外墙保暖，632000这个数用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·吉安期中) 如图所示几何体是由5个大小相同的小立方块搭成，它的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九下·吉安期中) 若 $\text{[math]}$ ．则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·吉安期中) 如图，二次函数 $\text{[math]}$ 的图象与x轴的一个交点坐标为 $\text{[math]}$ ，对称轴为直线 $\text{[math]}$ ，下列四个结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④当 $\text{[math]}$ 时， $\text{[math]}$ ；其中正确结论的个数为（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2024九下·吉安期中) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
8. (2024九下·吉安期中) 若 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，则 $\text{[math]}$ 的值是.

答案解析收藏纠错 + 选题
9. (2024九下·吉安期中) 已知 $\text{[math]}$ ， $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两个实数根，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
10. (2024九下·吉安期中) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的中位线，且 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点F．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024九下·吉安期中) 如图， $\text{[math]}$ 内接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
12. (2024九下·吉安期中) 如图，已知 $\text{[math]}$ 的半径为1，圆心P在抛物线 $\text{[math]}$ 上运动，当 $\text{[math]}$ 与x轴相切时，请写出所有符合条件的点P的坐标为．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题6分，共30分）

13. (2024九下·吉安期中)
1. （1）计算： $\text{[math]}$ ；
2. （2）如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
14. (2024九下·吉安期中) 解不等式组 $\text{[math]}$ ，把解集在数轴上表示出来．

答案解析收藏纠错 + 选题
15. (2024九下·吉安期中) 王强患有“红绿”色盲（分不清红色、绿色），星期天下午，晾晒袜子的架上有王强的2只红色运动袜、2只绿色运动袜（运动袜除颜色外其余均相同），王强要拿运动袜穿上去打篮球.
1. （1）王强从中任意拿一只运动袜是红色运动袜的事件是事件（填“必然”、“不可能”或“随机”）；
2. （2）求王强从中任意拿两只运动袜穿上，是同一种颜色运动袜的概率.
答案解析收藏纠错 + 选题
16. (2024九下·吉安期中) 如图，在 $\text{[math]}$ 的正方形网格中，每个小正方形的边长为1，小正方形的顶点叫做格点；圆 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个格点，请只用无刻度的直尺按下列要求分别作图（不写作法，保留作图痕迹）．
1. （1）在图1中，作出圆心 $\text{[math]}$ ；
2. （2）在图2中，在劣弧 $\text{[math]}$ 上找一点 $\text{[math]}$ ，使 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024·五莲模拟) 端午节是中国传统节日，人们有吃粽子的习俗．今年端午节来临之际，某商场预测A粽子能够畅销．根据预测，每千克A粽子节前的进价比节后多2元，节前用240元购进A粽子的数量比节后用相同金额购进的数量少4千克．根据以上信息，解答下列问题：
1. （1）该商场节后每千克A粽子的进价是多少元？
2. （2）如果该商场在节前和节后共购进A粽子400千克，且总费用不超过4600元，并按照节前每千克20元，节后每千克16元全部售出，那么该商场节前购进多少千克A粽子获得利润最大？最大利润是多少？
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共24分）

18. (2024九下·吉安期中) 如图矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ 、 $\text{[math]}$ 分别在 $\text{[math]}$ 轴和 $\text{[math]}$ 轴上，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 的中点 $\text{[math]}$ ，且与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求反比例函数的表达式及点 $\text{[math]}$ 的坐标．
2. （2）若点 $\text{[math]}$ 是 $\text{[math]}$ 边上的一点，且 $\text{[math]}$ 为等腰三角形，求直线 $\text{[math]}$ 的表达式．
答案解析收藏纠错 + 选题
19. (2024九下·吉安期中) 在日常生活中我们经常会使用到订书机，如图MN是装订机的底座，AB是装订机的托板，始终与底座平行，连接杆DE的D点固定，点E从A向B处滑动，压柄BC可绕着转轴B旋转．已知压柄BC的长度为15cm，BD＝5cm，压柄与托板的长度相等．
1. （1）当托板与压柄夹角∠ABC＝37°时，如图①点E从A点滑动了2cm，求连接杆DE的长度；
2. （2）当压柄BC从（1）中位置旋转到与底座AB的夹角∠ABC＝127°，如图②．求这个过程中点E滑动的距离．（答案保留根号）（参考数据：sin37°≈0.6，cos37°≈0.8．tan37°≈0.75）
答案解析收藏纠错 + 选题
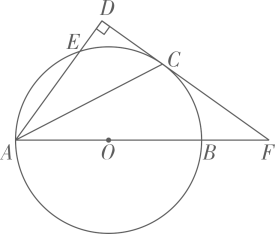
20. (2024九下·吉安期中) 如图，AB为⊙O的直径，E为⊙O上一点，点C为 $\text{[math]}$ 的中点，过点C作CD⊥AE，交AE的延长线于点D，延长DC交AB的延长线于点F．
1. （1）求证：CD是⊙O的切线；
2. （2）若DE=1，DC=2，求⊙ $\text{[math]}$ 的半径长．
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共18分）

21. (2024九下·吉安期中) 学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表，学生借阅图书的次数统计表
借阅图书的次数
0次
1次
2次
3次
4次及以上
人数
7
$\text{[math]}$
a
$\text{[math]}$
3
请你根据统计图表中的信息，解答下列问题：
1. （1） $\text{[math]}$ ， $\text{[math]}$ ．
2. （2）该调查统计数据的中位数是，众数是．
3. （3）请计算扇形统计图中“3次”所对应扇形的圆心角的度数．
4. （4）若学校共有 $\text{[math]}$ 名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．
答案解析收藏纠错 + 选题
22. (2024九下·吉安期中) 如图，抛物线 $\text{[math]}$ 与x轴交于A、B两点，与y轴交于点 $\text{[math]}$ ．
1. （1）求抛物线的对称轴及k的值；
2. （2）抛物线的对称轴上存在一点P，使得 $\text{[math]}$ 的值最小，求此时点P的坐标；
3. （3）点M是抛物线上一动点，且在第三象限，过点M作 $\text{[math]}$ 轴交线段AC于点P，求出线段PM长度的最大值．
答案解析收藏纠错 + 选题

六、解答题（本大题共12分）

23. (2024九下·吉安期中) 小新同学在数学探究课上，用几何画板进行了如下操作：首先画一个正方形 $\text{[math]}$ ，一条线段 $\text{[math]}$ $\text{[math]}$ ，再以点A为圆心， $\text{[math]}$ 的长为半径，画 $\text{[math]}$ 分别交 $\text{[math]}$ 于点E，交 $\text{[math]}$ 于点G，过点E，G分别作 $\text{[math]}$ 、 $\text{[math]}$ 的垂线交于点F，易得四边形 $\text{[math]}$ 也是正方形，连接 $\text{[math]}$ ．
1. （1）【探究发现】如图1，
  ① $\text{[math]}$ 与 $\text{[math]}$ 的大小关系：；
  ② $\text{[math]}$ 与 $\text{[math]}$ 的大小和位置关系：．
2. （2）【尝试证明】如图2，将正方形 $\text{[math]}$ 绕圆心A转动，在旋转过程中，上述①②中的关系还存在吗？请说明理由．
3. （3）【思维拓展】如图3，若 $\text{[math]}$ ，则：
  ①在旋转过程中，点B，A，G三点共线时， $\text{[math]}$ 的值为；
  ②在旋转过程中， $\text{[math]}$ 的最大值是．
答案解析收藏纠错 + 选题