贵州省黔东南州从江县庆云中学2024年中考一模数学试卷

更新时间：2024-07-22 浏览次数：3 类型：中考模拟

一、选择题：本题共12小题，每小题3分，共36分。在每小题给出的选项中，只有一项是符合题目要求的。

1. (2024·从江模拟) 在实数－1， $\text{[math]}$ ， $\text{[math]}$ ， 3.14中，无理数是（）

A . －1 B . $\text{[math]}$ C . $\text{[math]}$ D . 3.14

答案解析收藏纠错 + 选题
2. (2024·从江模拟) 一个立体图形的三视图如图所示，则该立体图形是（）

A . 圆柱 B . 圆锥 C . 长方体 D . 三棱柱

答案解析收藏纠错 + 选题
3. (2024·从江模拟) 金秋时节，贵阳市修文县种植的猕猴桃陆续成熟，果农和企业忙着采摘、分拣、包装猕猴桃，加工猕猴桃系列产品，供应市场 $\text{[math]}$ 目前，修文县猕猴桃种植面积达 $\text{[math]}$ 万亩，居全省第一、全国第三，已获得“国家地理标志保护产品”“国家级出口食品农产品质量安全示范区”等 $\text{[math]}$ 项荣誉 $\text{[math]}$ 将 $\text{[math]}$ 万这个数用科学记数法表示为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·从江模拟) 将一副三角板按如图所示摆放在一组平行线内， ∠1=25°， ∠2=30°，则∠3的度数为（）

A . 55° B . 65° C . 70° D . 75°

答案解析收藏纠错 + 选题
5. (2024·从江模拟) 某班级举办了一次背诵古诗竞赛，满分 $\text{[math]}$ 分，这次竞赛中，甲、乙两组学生成绩如下 $\text{[math]}$ 单位：分 $\text{[math]}$ ：甲组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；乙组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 比较两组数据的方差( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
6. (2024·从江模拟) 已知 $\text{[math]}$ ，计算 $\text{[math]}$ 的值是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·从江模拟) 祖国山河 $\text{[math]}$ 醉美贵州，贵州的山川秀丽，风景如画，每一处都是一幅诗意的画卷 $\text{[math]}$ 小王从家开车去贵州旅游，两地相距 $\text{[math]}$ 原计划平均速度为 $\text{[math]}$ ，实际平均速度提高了 $\text{[math]}$ ，结果提前 $\text{[math]}$ 小时到达 $\text{[math]}$ 由此可建立方程为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·从江模拟) 五一期间，商场推出购物有奖活动：如图，一个可以自由转动的转盘被平均分成六份，其中红色1份，黄色2份，绿色3份，转动一次转盘，指针指向红色为一等奖，指向黄色为二等奖，指向绿色为三等奖（指针指向两个扇形的交线时无效，需重新转动转盘）．转动转盘一次，获得一等奖的概率为（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·从江模拟) 已知点 $\text{[math]}$ 是等边 $\text{[math]}$ 的边 $\text{[math]}$ 上的一点，若 $\text{[math]}$ ，则在以线段 $\text{[math]}$ 为边的三角形中，最小内角的大小为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·从江模拟) 如图，点 $\text{[math]}$ 在正方形 $\text{[math]}$ 的对角线 $\text{[math]}$ 上， $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长，交边 $\text{[math]}$ 于点 $\text{[math]}$ ，交边 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2024·从江模拟) 梵净山翠峰茶，因主产于该县境内武陵山脉主峰 $\text{[math]}$ 梵净山而得名，是贵州省印江土家族苗族自治县所产茶叶品种之一 $\text{[math]}$ 如图为某商家近 $\text{[math]}$ 周的茶叶周销量 $\text{[math]}$ 罐 $\text{[math]}$ 一罐茶叶 $\text{[math]}$ 随时间 $\text{[math]}$ 周 $\text{[math]}$ 变化的图象，则下列说法错误的是( )

A . 第 $\text{[math]}$ 周销量最低，是 $\text{[math]}$ 罐 B . 在这 $\text{[math]}$ 周中，周销量增长速度最快的是第 $\text{[math]}$ 周到第 $\text{[math]}$ 周和第 $\text{[math]}$ 周到第 $\text{[math]}$ 周 C . 第 $\text{[math]}$ 周和第 $\text{[math]}$ 周的销量一样 D . 第 $\text{[math]}$ 周到第 $\text{[math]}$ 周，周销量 $\text{[math]}$ 罐 $\text{[math]}$ 随时间 $\text{[math]}$ 周 $\text{[math]}$ 的增大而增大

答案解析收藏纠错 + 选题
12. (2024·从江模拟) 如图，反比例函数 $\text{[math]}$ 的图象与过点 $\text{[math]}$ 的直线 $\text{[math]}$ 相交于 $\text{[math]}$ 、 $\text{[math]}$ 两点 $\text{[math]}$ 已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上任意一点 $\text{[math]}$ 如果 $\text{[math]}$ ，那么点 $\text{[math]}$ 的坐标为( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本题共4小题，每小题4分，共16分。

13. (2024·从江模拟) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2024·从江模拟) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，且 $\text{[math]}$ ，则实数 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024·从江模拟) 如图，直线 $\text{[math]}$ 为常数， $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 轴分别交于点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
16. (2024·从江模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的半径， $\text{[math]}$ 是 $\text{[math]}$ 的弦， $\text{[math]}$ 于点D， $\text{[math]}$ 是 $\text{[math]}$ 的切线， $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点E．若 $\text{[math]}$ ， $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题：本题共9小题，共98分。解答应写出文字说明，证明过程或演算步骤。

17. (2024·从江模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）解不等式组 $\text{[math]}$ ，请结合题意填空，完成本题的解答．
  （Ⅰ）不等式 $\text{[math]}$ ，得；
  （Ⅱ）解不等式 $\text{[math]}$ ，得；
  （Ⅲ）把不等式 $\text{[math]}$ 和 $\text{[math]}$ 的解集在数轴上表示出来；
  （Ⅳ）原不等式组的解集为．
答案解析收藏纠错 + 选题
18. (2024·从江模拟) 如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A-D-C，已知DC⊥BC，AB⊥BC，∠A=60°，AB=11m，CD=4m，求管道A-D-C的总长.

答案解析收藏纠错 + 选题
19. (2024·从江模拟) 某公司为提高服务质量，对其某个部门开展了客户满意度问卷调查，客户满意度以分数呈现，满意度从低到高为1分，2分，3分，4分，5分，共5档公司规定：若客户所评分数的平均数或中位数低于3.5分，则该部门需要对服务质量进行整改．工作人员从收回的问卷中随机抽取了20份，如图是根据这20份问卷中的客户所评分数绘制的统计图．
1. （1）求客户所评分数的中位数平均数，并判断该部门]是否需要整改．
2. （2）监督人员从余下的问卷中又随机抽取了1份，与之前的20份合在一起，重新计算后，发现客户所评分数的平均数大于3.55分，求监督人员抽取的问卷所评分数为几分．与(1)相比，中位数是否发生变化？
答案解析收藏纠错 + 选题
20. (2024·从江模拟) 如图，在 $\text{[math]}$ 中，已知 $\text{[math]}$ 为 $\text{[math]}$ 边上的中线，以 $\text{[math]}$ ， $\text{[math]}$ 为邻边作▱ $\text{[math]}$ ，连接 $\text{[math]}$ ，请你从方框中选择一个补充条件，使得四边形 $\text{[math]}$ 是菱形．
1. （1）你选择的补充条件是；可选条件 $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ；
2. （2）在 $\text{[math]}$ 的条件下，求证：四边形 $\text{[math]}$ 是菱形．
答案解析收藏纠错 + 选题
21. (2024·从江模拟) 某礼品店经销A，B两种礼品盒，第一次购进A种礼品盒10盒，B种礼品盒15盒，共花费2800元；第二次购进A种礼品盒6盒，B种礼品盒5盒，共花费1200元
1. （1）求购进A，B两种礼品盒的单价分别是多少元；
2. （2）若该礼品店准备再次购进两种礼品盒共40盒，总费用不超过4500元，那么至少购进A种礼品盒多少盒？
答案解析收藏纠错 + 选题
22. (2024·从江模拟) 如图，▱ $\text{[math]}$ 中，顶点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ， $\text{[math]}$ 轴，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象都经过 $\text{[math]}$ ， $\text{[math]}$ 两点．
1. （1）求 $\text{[math]}$ 的值．
2. （2）求▱ $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
23. (2024·从江模拟) 如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）判断 $\text{[math]}$ 的形状，并说明理由；
3. （3）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. (2024·从江模拟) 某校想将新建图书楼的正门设计为一个抛物线型门，并要求所设计的拱门的跨度与拱高之积为 $\text{[math]}$ ，还要兼顾美观、大方，和谐、通畅等因素，设计部门按要求价出了两个设计方案 $\text{[math]}$ 现把这两个方案中的拱门图形放入平面直角坐标系中，如图所示：
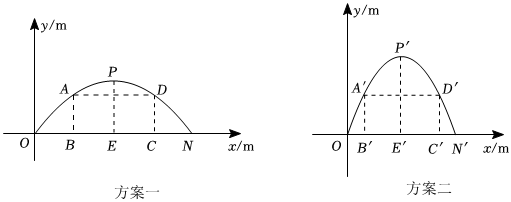
方案一，抛物线型拱门的跨度 $\text{[math]}$ ，拱高 $\text{[math]}$ 其中，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ ．

方案二，抛物线型拱门的跨度 $\text{[math]}$ ，拱高 $\text{[math]}$ 其中，点 $\text{[math]}$ 在 $\text{[math]}$ 轴上， $\text{[math]}$ ， $\text{[math]}$ ．

要在拱门中设置高为 $\text{[math]}$ 的矩形框架，其面积越大越好 $\text{[math]}$ 框架的粗细忽略不计 $\text{[math]}$ 方案一中，矩形框架 $\text{[math]}$ 的面积记为 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 在抛物线上，边 $\text{[math]}$ 在 $\text{[math]}$ 上；方案二中，矩形框架 $\text{[math]}$ 的面积记为 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，边 $\text{[math]}$ 在 $\text{[math]}$ 上 $\text{[math]}$ 现知，小华已正确求出方案二中，当 $\text{[math]}$ 时， $\text{[math]}$ ，请你根据以上提供的相关信息，解答下列问题：
1. （1）求方案一中抛物线的函数表达式；
2. （2）在方案一中，当 $\text{[math]}$ 时，求矩形框架 $\text{[math]}$ 的面积 $\text{[math]}$ 并比较 $\text{[math]}$ ， $\text{[math]}$ 的大小．
答案解析收藏纠错 + 选题
25. (2024·从江模拟)
1. （1）【阅读理解】如图 $\text{[math]}$ ，在矩形 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，由勾股定理，得 $\text{[math]}$ 同理 $\text{[math]}$ ，故AC $\text{[math]}$
2. （2）【探究发现】如图 $\text{[math]}$ ，四边形 $\text{[math]}$ 为平行四边形，若 $\text{[math]}$ ， $\text{[math]}$ ，则上述结论是否依然成立？请加以判断，并说明理由．
3. （3）【拓展提升】如图 $\text{[math]}$ ，已知 $\text{[math]}$ 为 $\text{[math]}$ 的一条中线， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
  求证： $\text{[math]}$ ．
4. （4）【尝试应用】如图 $\text{[math]}$ ，在矩形 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，则 $\text{[math]}$ 的最小值为．
答案解析收藏纠错 + 选题