一、单项选择题(本大题共12小题,每小题3分,共36分.每小题都给出四个选项中只有一个是正确的.考生用2B铅笔在答题卡上对应题目的答案标号涂黑.)
-
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
-
-
5.
(2024八下·港南期末)
王阿姨去超市买苹果,下表记录了5个数量值所对应的总价,其中
x表示数量,
y表示总价.根据表中的数据写出
y与
x的表达式为( )

| 1 | 2 | 3 | 4 | 5 | … |
 元 元
| 12 | 24 | 36 | 48 | 60 | … |
-
6.
(2024八下·港南期末)
已知样本容量为30,样本频数分布直方图中各小长方形的高的比依次是2∶4∶3∶1,则第二小组的频数是( )
A . 14
B . 12
C . 9
D . 8
-
A .  B . 1
C .
B . 1
C .  D . 3
D . 3
-
8.
(2024八下·港南期末)
如图,W对应的有序实数对为

, 有一个英文单词的字母,按顺序对应图中的有序实数对,分别为

, 则这个英文单词为( )

-
-
10.
(2024八下·港南期末)
图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )

A . 区域①处
B . 区域②处
C . 区域③处
D . 区域④处
-
A .  B . 2
C .
B . 2
C .  D . 3
D . 3
-
12.
(2024八下·港南期末)
如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形

与正方形

, 连结

若

,

, 则

的长为( )

二、填空题(本大题共6小题,每小题2分,共12分.)
-
-
-
-
-
-
18.
(2024八下·港南期末)
为了解八年级学生体能情况,随机抽查了其中的160名学生,测试了1分钟仰卧起坐的次数,并把数据按成绩分成四组,其中三组的频率分别为:

,

,

, 则剩下这组的学生有
人.
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
-
-
-
21.
(2024八下·港南期末)
某市在实行居民用水定额管理前,对居民生活用水情况进行了调查,如表是通过简单随机抽样调查获得的50个家庭去年的月均用水是(单位:t)
4.7 | 2.0 | 3.1 | 2.3 | 5.2 | 2.8 | 7.3 | 4.3 | 4.8 | 6.7 |
4.5 | 5.1 | 6.5 | 8.9 | 2.0 | 4.5 | 3.2 | 3.2 | 4.5 | 3.5 |
3.5 | 3.5 | 3.6 | 4.9 | 3.7 | 3.8 | 5.6 | 5.5 | 5.9 | 6.2 |
5.7 | 3.9 | 4.0 | 4.0 | 7.0 | 3.7 | 8.3 | 4.2 | 6.4 | 3.5 |
4.5 | 4.5 | 4.6 | 5.4 | 5.6 | 6.6 | 5.8 | 4.5 | 6.2 | 7.5 |
-
(1)
请选择合适的组距和组数.列出样本频数分布表,画出频数分布直方图;
-
(2)
为了鼓励节约用水,要确定一个用水量的标准,抽出这个标准的部分按1.5倍价格收费,若要使

的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?为什么?
-
-
-
(2)
请直接写出

的面积;
-
(3)
定义:在平面直角坐标系中,横坐标与纵坐标都是整数的点称为“整点”,请直接写出

内部所有的整点的坐标.
-
-
-
(2)
若AC平分∠DAB,AB=5,EC=2,求AE的长,
-
24.
(2024八下·港南期末)
水龙头关闭不紧会造成滴水,刘华同学用可以显示水量的容器做试验,并根据试验数据绘制出容器内盛水量

与滴水时间

的函数关系图象(如图).已知滴水的速度是

, 请结合图象解答下列问题:

-
-
(2)
求W与t之间的函数关系式,并计算在这种滴水状态下一天滴水的总量.
-
25.
(2024八下·港南期末)
综合与实践
某实践探究小组在放风筝时想测量风箏离地面的垂直高度,通过勘测,得到如下记录表:
测量示意图 | 
|
测量数据 | 边的长度 | ①测得水平距离 的长为15米. 的长为15米. |
②根据手中剩余线的长度计算出风筝线 的长为17米. 的长为17米. |
③小明牵线放风筝的手到地面的距离为1.7米. |
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度 . 请完成以下任务.
. 请完成以下任务.
-
(1)
已知:如图,在

中,

,

,

. 求线段

的长.
-
(2)
如果小明想要风筝沿

方向再上升12米,

长度不变,则他应该再放出多少米线?
-
26.
(2024八下·港南期末)
【阅读理解】我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而比较两个数或代数式的大小一般要进行转化,其中“作差法”就是常用的方法之一.其依据是不等式(或等式)的性质:若

, 则
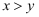
;若

, 则

;若

, 则

.
例:已知 ,
,  . 其中
. 其中 , 求证:
, 求证: .
.
证明: ,
,
因为 , 所以
, 所以 , 故
, 故 .
.
-
(1)
【新知理解】比较大小:


. (填“>”,“=”,“<”)
-
(2)
【问题解决】甲、乙两个平行四边形,其底和高如图所示

, 其面积分别为

,

, 请比较

,

的大小关系.

-
(3)
【拓展应用】小亮和小莹同去一家水果店购买苹果,两人均购买了两次,两次购买苹果的单价不同,两人的购货方式也不同.小亮每次购买1千克,小莹每次花10元钱购买.设两人第一次购买苹果的单价均为
m元/千克,第二次购买苹果的单价均为
n元/千克(
m ,
n是正数,且

),试分析小莹和小亮谁的购货方式更合算?


. 请完成以下任务.
,
. 其中
, 求证:
.
,
, 所以
, 故
.
