河北省保定市曲阳县2023-2024学年八年级下学期期末数学...

更新时间：2024-08-07 浏览次数：19 类型：期末考试

一、选择题（本大题有16个小题，共42分，1~10小题，每小题3分，11~16小题，每小题2分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024八下·曲阳期末) 某中学运动社团想要统计最受本校学生欢迎的北京冬奥会运动项目，以下是打乱的统计步骤：
①据统计表绘制条形统计图；
②制作调查问卷，对全校同学进行问卷调查；
③从条形统计图中分析出最受欢迎的冬奥会项目；
④整理问卷调查数据，并绘制统计表.
统计步骤的正确排顺为（）

A . ④③②① B . ②④①③ C . ②①③④ D . ②④③①

答案解析收藏纠错 + 选题
2. (2024八下·曲阳期末) 如图给出了四边形 $\text{[math]}$ 的部分数据，若使得四边形 $\text{[math]}$ 为平行四边形，还需要添加的条件可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·曲阳期末) 定义新运算： $\text{[math]}$ ，则对于函数 $\text{[math]}$ ，下列说法正确的是（）

A . 该函数图象经过点 $\text{[math]}$ B . 该函数不经过第四象限 C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . $\text{[math]}$ 随 $\text{[math]}$ 增大而减小

答案解析收藏纠错 + 选题
4. (2024八下·曲阳期末) 一个多边形的内角和等于它的外角和的3倍，则它是（）边形.

A . 六 B . 七 C . 八 D . 九

答案解析收藏纠错 + 选题
5. (2024八下·曲阳期末) 如图，在平行四边形 $\text{[math]}$ 中，DE是 $\text{[math]}$ 的平分线，F是AB的中点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . 4：1：2 B . 4：1：3 C . 3：1：2 D . 5：1：2

答案解析收藏纠错 + 选题
6. (2024八下·曲阳期末) 如图1，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于 $\text{[math]}$ ，要在对角线 $\text{[math]}$ 上找两点 $\text{[math]}$ 、 $\text{[math]}$ ，使得四边形 $\text{[math]}$ 是菱形，现有图2中的甲、乙两种方案，则正确的方案是（）

A . 只有甲 B . 只有乙 C . 甲和乙 D . 甲乙都不是

答案解析收藏纠错 + 选题
7. (2024八下·曲阳期末) 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 厘米， $\text{[math]}$ 厘米，点 $\text{[math]}$ 从点 $\text{[math]}$ 出发以每秒 $\text{[math]}$ 厘米的速度，沿 $\text{[math]}$ 在平行四边形的边上匀速运动至点 $\text{[math]}$ ．设点 $\text{[math]}$ 的运动时间为 $\text{[math]}$ 秒， $\text{[math]}$ 的面积为 $\text{[math]}$ 平方厘米，下列图中表示 $\text{[math]}$ 与 $\text{[math]}$ 之间函数关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2024八下·曲阳期末) 已知甲车从A地出发前往B地，同时乙车从B地出发前往A地，两车离A地距离y（千米）和行驶时间x（小时）的关系如图，则两车相遇时，甲车行驶的时间是（）

A . 2小时 B . $\text{[math]}$ 小时 C . $\text{[math]}$ 小时 D . 3小时

答案解析收藏纠错 + 选题
9. (2024八下·曲阳期末) 物理课上，于老师让同学们做这样的实验：在放水的盆中放入质地均匀的木块 $\text{[math]}$ ，再在其上方放置不同质量的铁块 $\text{[math]}$ ．已知木块 $\text{[math]}$ 全程保持漂浮状态，通过测量木块 $\text{[math]}$ 浮在水面上的高度 $\text{[math]}$ 与铁块 $\text{[math]}$ 的质量 $\text{[math]}$ ，可得它们之间满足一次函数关系，据此可知当铁块 $\text{[math]}$ 质量为 $\text{[math]}$ 时，木块 $\text{[math]}$ 浮在水面上的高度 $\text{[math]}$ 为（　　）
实验次数
一
二
三
铁块 $\text{[math]}$ 质量 $\text{[math]}$
25
50
75
高度 $\text{[math]}$
44
38
32

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八下·曲阳期末) 如图，已知矩形ABCD的对角线AC的长为10cm，连结矩形各边中点E、F、G、H得四边形EFGH，则四边形EFGH的周长为（）cm．

A . 20 B . $\text{[math]}$ C . $\text{[math]}$ D . 25

答案解析收藏纠错 + 选题
11. (2024八下·曲阳期末) 如图，函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ ，则不等式组 $\text{[math]}$ 的整数解有（）个．

A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
12. (2024八下·曲阳期末) 中考体育篮球运球考试中，测试场地长20米，宽7米，起点线后5米处开始设置10根标志杆，每排设置两根，各排标志杆底座中心点之间相距1米，距两侧边线3米，假设某学生按照图1路线进行单向运球，运球行进过程中，学生与测试老师的距离y与运球时间x之间的图象如图2所示，那么测试老师可能站在图1中的位置为（）

A . 点A B . 点B C . 点C D . 点D

答案解析收藏纠错 + 选题
13. (2024八下·曲阳期末) 如图，在 $\text{[math]}$ 中，D ， E分别为AB ， AC的中点，连接DE ，点F在DE上且 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，则线段EF的长为（）

A . 3 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
14. (2024八下·曲阳期末) 出入相补原理是我国古代数学的重要成就之一，最早是由三国时期数学家刘徽创建，“将一个几何图形，任意切成多块小图形，几何图形的总面积保持不变，等于所分割成的小图形的面积之和“是该原理的重要内容之一，如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线AC与BD交于点O ，点E为BC边上一点， $\text{[math]}$ ， $\text{[math]}$ ，垂足分别为点F ， G ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2024八下·曲阳期末) 三名快递员某天的工作情况如图所示，其中点A₁ ， A₂ ， A₃的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数；点B₁ ， B₂ ， B₃的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数．
有如下四个结论：
①上午派送快递所用时间最短的是甲；
②下午派送快递件数最多的是丙；
③在这一天中派送所用时间最长的是乙；
④在这一天中派送快递总件数最多的是乙．
上述结论中，所有正确结论的序号是（）

A . ①④ B . ①③④ C . ②③ D . ①②③④

答案解析收藏纠错 + 选题
16. (2024八下·曲阳期末) 如图，正方形 $\text{[math]}$ 中，E、F分别为AB、AD上的点， $\text{[math]}$ ， CE、BF交于H ， BF交AC于M ， O为AC的中点，OB交CE于N ，连OH.下列结论中：
① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ .其中正确的命题（）

A . 只有①② B . 只有①②④ C . 只有①④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共9分.）

17. (2024八下·曲阳期末) 一个俱乐部里只有两种成员：一种是老实人，永远说真话；一种是骗子，永远说假话．某天俱乐部的全体成员围坐成一圈，每个老实人两旁都是骗子，每个骗子两旁都是老实人．外来一位记者问俱乐部的成员张三：“俱乐部里共有多少成员？”张三答：“共有45人．”另一个成员李四说：“张三是老实人．”据此可判断李四是 $\text{[math]}$ 填“老实人”或“骗子” $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024八下·曲阳期末) 某超市糯米的价格为5元/千克，端午节推出促销活动：一次购买的数量不超过2千克时，按原价售出，超过2千克时，超过的部分打8折.若某人付款14元，则他购买了千克糯米；设某人的付款金额为x元，购买量为y千克，则购买量y关于付款金额 $\text{[math]}$ 的函数表达式为.

答案解析收藏纠错 + 选题
19. (2024八下·曲阳期末) 如图，在平面直角坐标系中， $\text{[math]}$ 为坐标原点， $\text{[math]}$ 为 $\text{[math]}$ 轴上一点，菱形 $\text{[math]}$ 的边长为2， $\text{[math]}$ ，点D是OB边上一动点（不与点O ， B重合），点E在BC边上，且 $\text{[math]}$ ，下列结论：
① $\text{[math]}$ ；② $\text{[math]}$ 的大小随点 $\text{[math]}$ 的运动而变化；③直线BC的解析式为 $\text{[math]}$ ；④DE的最小值为 $\text{[math]}$ .其中正确的有.（填写序号）

答案解析收藏纠错 + 选题

三、解答题（共69分解答应写出文字说明、证明过程或演算步骤.）

20. (2024八下·曲阳期末) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
21. (2024八下·曲阳期末) 如下表是一次函数 $\text{[math]}$ （k ， b为常数， $\text{[math]}$ ）中. $\text{[math]}$ 与 $\text{[math]}$ 的两组对应值，求这个一次函数的表达式.
x
$\text{[math]}$
0
y
6
3

答案解析收藏纠错 + 选题
22. (2024八下·曲阳期末) 如图，是由小正方形组成的 $\text{[math]}$ 网格，每个小正方形的顶点叫做格点， $\text{[math]}$ 的三个顶点都是格点，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，仅用无刻度的直尺在给定网格中完成画图．（画图过程用虚线表示，画图结果用实线表示）．
1. （1）在图（1）中，以 $\text{[math]}$ 为边画平行四边形 $\text{[math]}$ ，再将线段 $\text{[math]}$ 平移到 $\text{[math]}$ ，使点 $\text{[math]}$ 与点 $\text{[math]}$ 对应，点 $\text{[math]}$ 与点 $\text{[math]}$ 对应，画出线段 $\text{[math]}$ ；
2. （2）在图（2）中，过点 $\text{[math]}$ 画 $\text{[math]}$ ，且 $\text{[math]}$ ，再在 $\text{[math]}$ 上找点 $\text{[math]}$ ，使 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2024八下·曲阳期末) 杭州亚运会于2023年9月23日召开，某校决定在全校范围内开展亚运知识的宣传教育活动.为了了解宣传效果，随机抽取部分学生，并在活动前、后对这些学生进行了两次跟踪测评，两次测评中所有同学的成绩没有低于30分的，现在将收集的数据制成如下的频数分布直方图（每一组包含左端值，不包含右端值）和频数分布表
宣传活动后亚运知识成绩频数分布表
成绩/分
30~40
40~50
50~60
60~70
70~80
80~90
90~100
频数
2
6
6
16
m
30
12
1. （1）本次活动共抽取名学生.
2. （2）在频数分布直方图中，组距是；
3. （3）表中的 $\text{[math]}$ ，宣传活动后，在抽取的学生中分数高于65分的至少有人，至多有人.
4. （4）小聪认为，宣传活动后成绩在60~70分的人数为16，比活动前减少了14人，因此学校开展的宣传活动没有效果，请你结合统计图表，说一说小聪的看法是否正确，为什么？
答案解析收藏纠错 + 选题
24. (2024八下·曲阳期末) 如图，在△ABC中，D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．
1. （1）求证：四边形ADEF是平行四边形；
2. （2）求证：∠DHF=∠DEF．
答案解析收藏纠错 + 选题
25. (2024八下·曲阳期末) 如图，在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ 的值；
2. （2）过第二象限的点 $\text{[math]}$ 作平行于 $\text{[math]}$ 轴的直线，交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，交直线 $\text{[math]}$ 于点 $\text{[math]}$ .
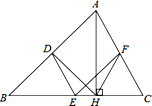
  ①当 $\text{[math]}$ 时，用等式表示线段PC与PB的数量关系，并说明理由；
  ②当 $\text{[math]}$ 时，结合函数的图象则有PC_▲_ $\text{[math]}$ （填“>”，“<”或“=”）.
答案解析收藏纠错 + 选题
26. (2024八下·曲阳期末) 定义：若四边形中某个顶点与其他三个顶点的距离相等，则这个四边形叫做等距四边形，这个顶点叫做这个四边形的等距点.
1. （1）判断：如图①，一个内角为60°的菱形_▲_等距四边形.（填“是”或“不是”）并说明为什么？
2. （2）如图②，在5×5的网格图（每个小正方形的边长为1）中有A、B两点，请在给出的两个网格图上各找出C、D两个格点，使得以A、B、C、D为顶点的四边形是以点A为等距点的“等距四边形”，画出相应的“等距四边形”（互不全等），并求出该等距四边形的端点均为非等距点的对角线长.
答案解析收藏纠错 + 选题