一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
-
-
A . 43
B . 46
C . 37
D . 36
-
A . 1
B .  C . 11
D . 15
C . 11
D . 15
-
5.
(2024高二下·新疆维吾尔自治区期中)
某学校为参加辩论比赛,选出8名学生,其中3名男生和5名女生,为了更好备赛和作进一步选拔,现将这8名学生随机地平均分成两队进行试赛,那么两队中均有男生的概率是( )
-
6.
(2024高二下·新疆维吾尔自治区期中)
一艘海监船上配有雷达,其监测范围是半径为26 km的圆形区域,一艘外籍轮船从位于海监船正东40 km的A处出发径直驶向位于海监船正北30km的B处岛屿,船速为10 km/h这艘外籍轮船能被海监船监测到且持续时间长约为( ) 小时
A . 1
B . 2
C . 3
D . 4
-
-
二、多项选择题:本题共3小题,每小题6分,共18分.
三、填空题:本题共3小题,每小题5分,共15分.
四、解答题共5小题,15小题13分,16,17小题各15分,18,19小题各17分.
-
-
(1)
求

;
-
(2)
求

的单调区间和极值.
-
16.
(2024高二下·新疆维吾尔自治区期中)
本学期初,某校为检验高三学生网络学习的效果,对全校高三学生进行期初数学测试(满分100),并从中随机抽取了100名学生的成绩,以此为样本,分成

,

,

,

,

五组,得到如图所示频率分布直方图.

-
(1)
求图中

的值;
-
(2)
估计该校高三学生期初数学成绩的平均数和85%分位数;
-
(3)
为进一步了解学困生的学习情况,从数学成绩低于70分的学生中,分层抽样6人,再从6人中任取2人,求此2人分数都在

的概率.
-
-
(1)
求证:

平面

;
-
(2)
求证:平面

平面

;
-
(3)
求
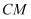
与平面

所成角的正弦值.
-
-
(1)
求

.
-
(2)
求

的通项公式;
-
-
19.
(2024高二下·新疆维吾尔自治区期中)
已知椭圆

的左,右焦点分别为

, 且

与短轴的一个端点

构成一个等腰直角三角形,点

在椭圆

上,过点

作互相垂直且与

轴不重合的两直线

分别交椭圆

于

, 且

分别是弦

的中点.
-
-
(2)
求证:直线

过定点;
-
(3)
求

面积的最大值.

