一、选择题: (本大题共16个小题, 共38分.1~6小题各3分, 7~16小题各2分. 在每小题给出的四个选项中,只有一项是符合题目要求的
-
1.
(2023七上·滦州期中)
检测 4 个足球,其中超过标准的克数记为正数,不足的克数记为负数. 从轻重的角度看,哪个球更接近标准( )
A . -0.8
B . +1.8
C . -3.2
D . -1.7
-
A . a+3
B .  C . 0
D . x>y
C . 0
D . x>y
-
A .  B .
B .  C . 2023
D . 一2023
C . 2023
D . 一2023
-
4.
(2023七上·滦州期中)
如图, 将甲, 乙两把尺子拼在一起, 两端重合, 如果甲尺经校定是直的,那么乙尺不是直的,判断依据是( )

A . 两点之间直线最短
B . 经过一点有一条直线,并且只有一条直线
C . 线段可以向两个方向延长
D . 经过两点有一条直线,并且只有一条直线
-
-
A . -7×6
B . (-8)-15
C . 0×(-4)×(-5)
D . (-2)+6
-
A . 75°
B . 85°
C . 105°
D . 135°
-
A . x除以y加3
B . y加3除x
C . y与3的和除以x
D . x除以y与3的和所得的商
-
A . -5
B . 1
C . 5或 -1
D . -5 或 1
-
-
A . 40.11°
B . 40.21°
C . 40.16°
D . 40.26°
-
A . 点B与点D
B . 点A与点C
C . 点A与点D
D . 点B与点C
-
13.
(2023七上·滦州期中)
如图为O、 A、 B、C四点在数轴上的位置图,其中O为原点,且AC=1,OA=OB,若点C所表示的数为x,则点B所表示的数为( )

A . -(x+1)
B . -(x-1)
C . x+1
D . x-1
-
A . 54° 40'
B . 54° 20'
C . 144° 40'
D . 144° 20'
-
-
16.
(2023七上·滦州期中)
如图,矩形纸片 ABCD,M为AD边的中点将纸片沿BM、CM折叠,使 A 点落在 A
1处, D点落在 D
1处, 若∠1=40°, 则∠BMC=( )

A . 75°
B . 110°
C . 120°
D . 140°
二、填空题:(本大题共3个小题,共10分.每空2分
-
17.
(2023七上·滦州期中)
在(-1)
5、 (-1)
4、-2
4 , (-3)
2这四个数中, 负数有
个, 比较这四个数的大小(用“>”连接)
。
-
-
19.
(2023七上·滦州期中)
观察: 等式① 2=1 ×2
等式② 2+ 4=2×3=6
等式③ 2+4 +6=3×4=12
等式④ 2+4 + 6 + 8=4×5=20
仿照以上等式写出等式⑥; 则 26+ 28 + + 50=。
三、解答题:(本大题共7个小题,共72分。解答过程应写出文字说明、证明过程或演算步骤
-
-
-
(2)
在这四个数中选出两个数,按下列要求列出算式并计算:
①两数差的结果最小:
②两数积的结果最大:
-
(3)
请在□内填上+, -, ×, ÷中的某一个, 使等式-8□ (1□3)=-2成立.
-
-
-
(2)
若∠BAE=60° , 直接写出旋转角的度数;
-
-
-
-
(2)
若D是AB的中点,E是AC的中点,求DE的长.
-
-
(1)
表中第6行的最后一个数是,它是自然数的平方,第7行第2个数是,第7行共有个数;
-
(2)
第n行的最后一个数是
,第n+l行第5个数是
(n>3),第n+l行共有
个数(用含n代数式表示); 1
2 3 4
5 6 7 8 9
l0 ll 12 13 14 15 l6
……
-
24.
(2023七上·滦州期中)
老师设计了接力游戏,用合作的方式完成有理数运算,规则是:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:

-
(1)
找出此次接力中计算错误的学生,并写出他们所出现错误之处的正确结果;
-
(2)
计算:

请同学们注意计算细节呀.
-
25.
(2023七上·滦州期中)
操作与尝试:在纸面上有如图所示的一数轴,折叠纸面,若数轴上表示Ⅰ的点与表示-I的点重合,则数轴上表示-2的点与表示2的点重合,此时折点表示的数为0 。

探究与应用:现打开纸面后,重新折叠,使数轴上表示-4的点与表示0的点重合,数轴上A、B两点折叠后重合,M、N两点折叠后重合。
-
(1)
则数轴上表示3的点与此时折点的距离是,表示3的点与表示的点重合;
-
(2)
若点A到原点的距离是5个单位长度,求B点表示的数;
-
(3)
若数轴上M、N两点之间的距离为a,如果M点表示的数比N点表示的数大,直接写出M点表示的数(用含a的代数式表示)。
-
26.
(2023七上·滦州期中)
如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°. 将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线 OB上,另一边 ON在直线AB的下方。

-
(1)
将图1中的三角板绕点O逆时针旋转至图2, 使一边 OM在∠BOC的内部, 且恰好平分∠BOC. 求∠BON的度数。
-
(2)
将图1中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为(直接写出结果).
-
(3)
将图Ⅰ中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM-

'的值。

 B .
B . 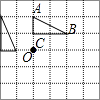 C .
C . 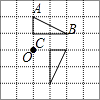 D .
D . 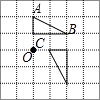

![]()



![]()
