1. (2020·建邺模拟) （概念认识）

若以三角形某边上任意一点为圆心，所作的半圆上的所有点都在该三角形的内部或边上，则将符合条件且半径最大的半圆称为该边关联的极限内半圆.

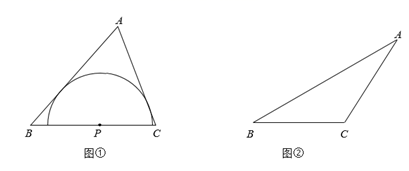
如图①，点P是锐角△ABC的边BC上一点，以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时，半圆P为边BC关联的极限内半圆.

 

1. （1） （初步思考）若等边△ABC的边长为1，则边BC关联的极限内半圆的半径长为.
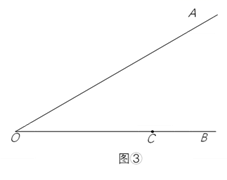
3. （2） 如图②，在钝角△ABC中，用直尺和圆规作出边BC关联的极限内半圆（保留作图痕迹，不写作法）.
5. （3） （深入研究）如图③，∠AOB＝30°，点C在射线OB上，OC＝6，点Q是射线OA上一动点.在△QOC中，若边OC关联的极限内半圆的半径为r，当1≤r≤2时，求OQ的长的取值范围.