1. (2020·吉安模拟) 定义：两个相似等腰三角形，如果它们的底角有一个公共的顶点，那么把这两个三角形称为“关联等腰三角形”．如图，在 与 中， ，且 所以称 与 为“关联等腰三角形”，设它们的顶角为 ，连接 ，则称 会为“关联比"．

下面是小颖探究“关联比”与α之间的关系的思维过程，请阅读后，解答下列问题：

[特例感知]

1. （1） 当 与 为“关联等腰三角形”，且 时，

   ①在图1中，若点E落在 上，则“关联比” =      ▲      

   

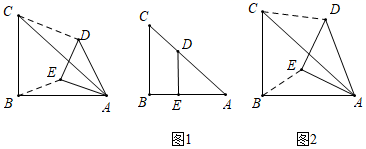
   ②在图2中，探究 与 的关系，并求出“关联比” 的值．

   

3. （2） [类比探究]

   如图3，

   ①当 与 为“关联等腰三角形”，且 时，“关联比” =

   ②猜想：当 与 为“关联等腰三角形”，且 时，“关联比” = (直接写出结果，用含 的式子表示)

5. （3） [迁移运用]

   如图4， 与 为“关联等腰三角形”．若 点 为 边上一点，且 ，点E为 上一动点，求点E自点B运动至点P时，点D所经过的路径长．