
 B .
B .  C .
C .  D .
D . 

A . 抽到的是小宁最终想要看的一场比赛的球桌号
B . 抽到的是父亲最终想要看的一场比赛的球桌号
C . 小宁和父亲抽到同一个球桌号
D . 小宁和父亲抽到的球桌号不一样
|
成绩 |
3′40″及以下 |
3′41″-4′ |
4′01″-4′20″ |
4′21″-4′40″ |
4′41″及以上 |
|
等级 |
A |
B |
C |
D |
E |
|
百分比 |
10% |
25% |
m |
20% |
n |


①求此时点B到地面的距离;
②若斜射阳光与BC所在直线垂直时,求BC在水平地面上投影的长度约是多少.(说明: ≈1.732,结果精确到0.1m)

①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= ▲ °时,DM与⊙O相切.
| x | … | -4 | -3 | -2 | -1 | | | | | | | 1 | 2 | 3 | 4 | … |
| y | … | | | | | | | | | | | 2 | | | | … |

观察函数图象,回答下列问题:
A . 既是轴对称图形,又是中心对称图形 B . 只是轴对称图形,不是中心对称图形
C . 不是轴对称图形,而是中心对称图形 D . 既不是轴对称图形,也不是中心对称图形
在x<0时,当x=时,函数y有最(大,小)值,且这个最值等于;
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
①在图1中,若点E落在 上,则“关联比”
= ▲
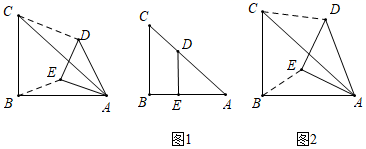
②在图2中,探究 与
的关系,并求出“关联比”
的值.

如图3,
①当 与
为“关联等腰三角形”,且
时,“关联比”
=
②猜想:当 与
为“关联等腰三角形”,且
时,“关联比”
= (直接写出结果,用含
的式子表示)
如图4, 与
为“关联等腰三角形”.若
点
为
边上一点,且
,点E为
上一动点,求点E自点B运动至点P时,点D所经过的路径长.
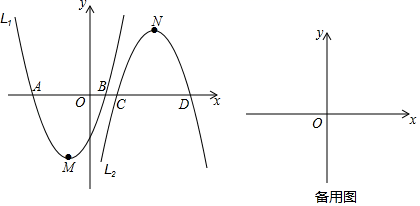
①求所有定点的坐标;
②若抛物线L1位置固定不变,通过左右平移抛物线L2的位置使这些定点组成的图形为菱形,则抛物线L2应平移的距离是多少?