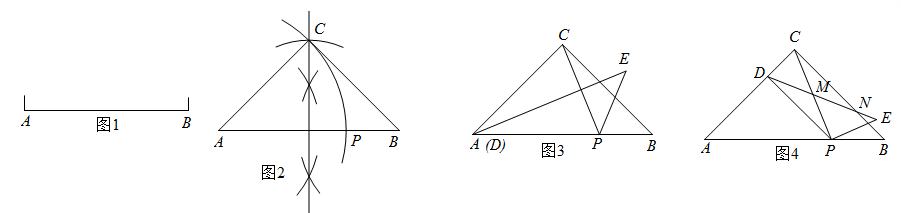
①如图3,当点D运动到点A时,求∠CPE的度数.
②如图4,DE分别交CP,CB于点M,N,当点D为线段AC的“趣点”时(CD<AD),猜想:点N是否为线段ME的“趣点”?并说明理由.

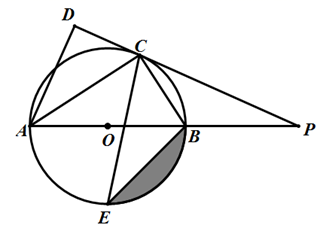
①若2AO=3OE,求AB
②若△AEC为等腰直角三角形,且∠EAC=90°,求四边形BDOE的面积.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.

①求的值;
②延长交
于点G.交
于点F.求
.
如图2,在四边形中,点D是
边的中点,连接
、
,
, 若
, 求线段
的长;
某市进行绿化改造,美化生态环境.如图3,现有一块三角形的荒地计划改造公园,经测量
米,
, 按设计要求,要在三角形公园
内建造一个以A为直角顶点的等腰直角三角形活动场所
, 且顶点D、顶点E分别在边
、
上,且
米,请求出符合设计要求的等腰直角三角形活动场所
的顶点D所在的位置(即
的长).
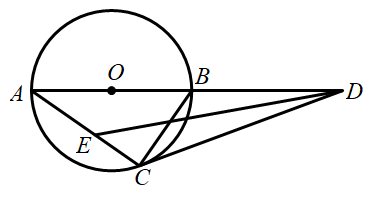

①求证:AM=CM,AM⊥CM;
②若AB=4,求△AOM的面积.


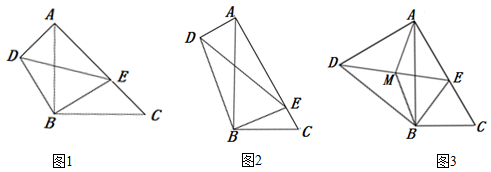
如图1,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=45°,点E是线段AC上一动点,连接DE.
填空:①则 的值为;②∠EAD的度数为.
如图2,在Rt△ABC和Rt△DBE中,∠ABC=∠DBE=90°,∠ACB=∠BED=60°,点E是线段AC上一动点,连接DE.请求出 的值及∠EAD的度数;
如图3,在(2)的条件下,取线段DE的中点M,连接AM、BM,若BC=4,则当△ABM是直角三角形时,求线段AD的长.
①如果正方形 绕点
旋转,连接
、
、
,线段
与AF的数量关系有无变化?请仅就图2的情形给出证明;
②正方形 绕点
旋转的过程中,当以点A,B,C,E为顶点的四边形是平行四边形时.直接写出线段AF的长.

如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
填空:① 的度数是;②线段AD,BE之间的数量关系为;
如图2,△ABC和△CDE均为等腰直角三角形, ,
,
,直线AD和直线BE交于点F.请判断
的度数及线段AD,BE之间的数量关系,并说明理由.
如图3,在△ABC中, ,
,
,点D在AB边上,
于点E,
,将△ADE绕着点A在平面内旋转,请直接写出直线DE经过点B时,点C到直线DE的距离.
①求 的长度.
② 为边
上一点,以
、
、
中的两点及点
为顶点的三角形为等腰三角形,直接写出
的长度.

特例探索
②如图2,当 ,
时,求a和b的值.
在菱形ABCD中,对角线 ,
, O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求
的值.
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
①在图1中,若点E落在 上,则“关联比”
= ▲
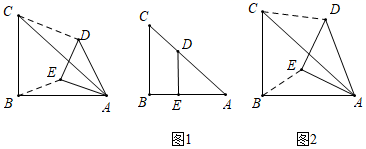
②在图2中,探究 与
的关系,并求出“关联比”
的值.

如图3,
①当 与
为“关联等腰三角形”,且
时,“关联比”
=
②猜想:当 与
为“关联等腰三角形”,且
时,“关联比”
= (直接写出结果,用含
的式子表示)
如图4, 与
为“关联等腰三角形”.若
点
为
边上一点,且
,点E为
上一动点,求点E自点B运动至点P时,点D所经过的路径长.