1. (2021·李沧模拟) （问题）用n边形的对角线把n边形分割成（n-2个三角形，共有多少种不同的分割方案 ？

（探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进转化，最后猜想得出结论．不妨假设n边形的分割方案有 种．

探究一：用四边形的对角线把四边形分割成2个三角形，共有多少种不同的分割方案？如图①，图②，显然，只有2种不同的分割方案．所以， ．

探究二：用五边形的对角线把五边形分割成3个三角形，共有多少种不同的分割方案？不妨把分割方案分成三类：

第1类：如图③，用点 ， 与 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有 种不同的分割方案，所以，此类共有 种不同的分割方案．

第2类：如图④，用点 ， 与 连接，把五边形分割成3个三角形，有1种不同的分割方案，可视为 种分割方案．

第3类：如图⑤，用点 ， 与 连接，先把五边形分割转化成1个三角形和1个四边形，再把四边形分割成2个三角形，由探究一知，有f（4）种不同的分割方案，所以，此类共有f（4）种不同的分割方案．

所以， （种）

探究三：用六边形的对角线把六边形分割成4个三角形，共有多少种不同的分割方案？不妨把分割方案分成四类：

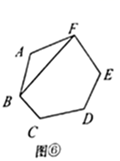
第1类：如图⑥，用 ， 与 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 种不同的分割方案，所以，此类共有 种不同的分割方案．

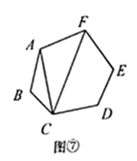
第2类：如图⑦，用 ， 与 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 种不同的分割方案．所以，此类共有 种分割方案．

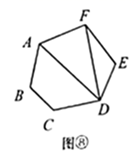
第3类：如图⑧，用 ， 与 连接，先把六边形分割转化成2个三角形和1个四边形．再把四边形分割成2个三角形，由探究一知，有 种不同的分割方案．所以，此类共有 种分割方案．

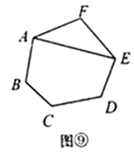
第4类：如图，用 ， 与 连接，先把六边形分割转化成1个三角形和1个五边形，再把五边形分割成3个三角形，由探究二知，有 种不同的分割方案．所以，此类共有 种分割方案．

所以，

（种）

探究四：用七边形的对角线把七边形分割成5个三角形，则 与 的关系为 ，共有种不同的分割方案．

……

（结论）用 边形的对角线把 边形分割成 个三角形，共有多少种不同的分割方案 ？（直接写出 与 之间的关系式，不写解答过程）

（应用）用九边形的对角线把九边形分割成7个三角形，共有多少种不同的分割方案？（应用上述结论中的关系式求解）