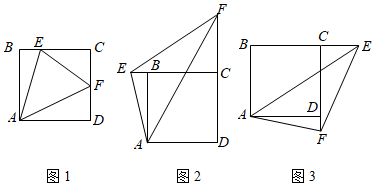
问题:如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证:
.
观察:EF、DF、BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?
思路:将 绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的
.
①根据上述思路在图1中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?(写出详细的解答过程)
若点E、F分别为正方形两条边的延长线上的动点,EF、BE、DF三者之间还存在(1)中的关系吗?根据解决(1)中问题的经验加以探究.
①如图2,在正方形ABCD中,点E、F分别是CB、DC延长线上的动点,且 ,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.
②如图3,在正方形ABCD中,点E、F分别是BC、CD延长线上的动点,且 ,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).