
①若DF=BF+2EF,求证:AE=BE.
②设四边形AEFD和 的面积分别是
和
,若
,求线段BF的长.

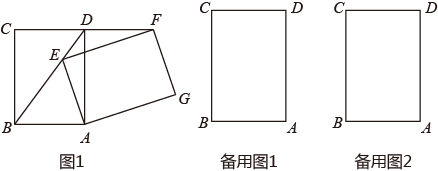
①求证:∠BEA=∠BDC;
②连接AF,判断四边形BAFD的形状,并说明理由
②容易发现,当 时,
;当
时,
.由此可见,图象在第 ▲ 象限;
③阅读材料:当 时,
.当
时,即
,
有最小值是2.请仿照上述过程,求出当
时,
的最大值;

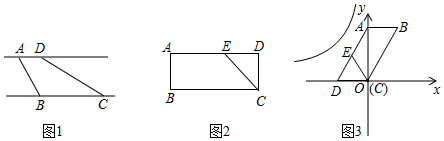
将 两边同时乘以
并移项,得到
,两边再同时加上
,得( ▲ )2
.请用这样的方法解方程:
;
(从这里可以看出方程的解为
,
)
即
因为 ,所以
、
的平均数为
,不妨设
,
,
利用 ,得
,所以
,即能求出
的值.
举例如下:解一元二次方程 ,由于
,所以方程的两个根为
,而
,解得
,所以方程的解为
,
.
请运用以上方法解如下方程① ;②

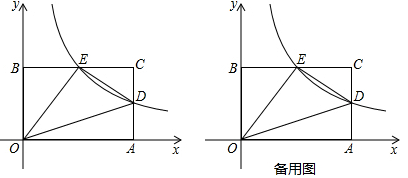
①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
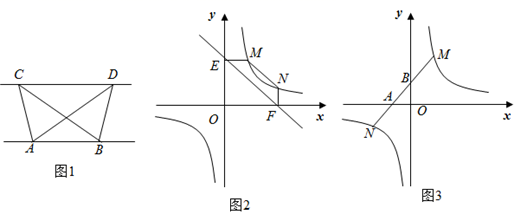



求证:四边形AECD为单等对边四边形;
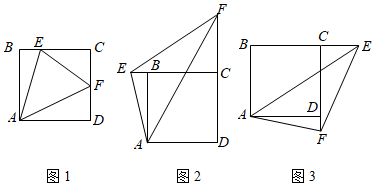
问题:如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证:
.
观察:EF、DF、BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?
思路:将 绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的
.
①根据上述思路在图1中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?(写出详细的解答过程)
若点E、F分别为正方形两条边的延长线上的动点,EF、BE、DF三者之间还存在(1)中的关系吗?根据解决(1)中问题的经验加以探究.
①如图2,在正方形ABCD中,点E、F分别是CB、DC延长线上的动点,且 ,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.
②如图3,在正方形ABCD中,点E、F分别是BC、CD延长线上的动点,且 ,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).
①判定 的形状,并说明理由;
②点 在运动的过程中,
和
的度数和是否变化?如果变化,说明理由;如果不变,求出
和
的度数和.

