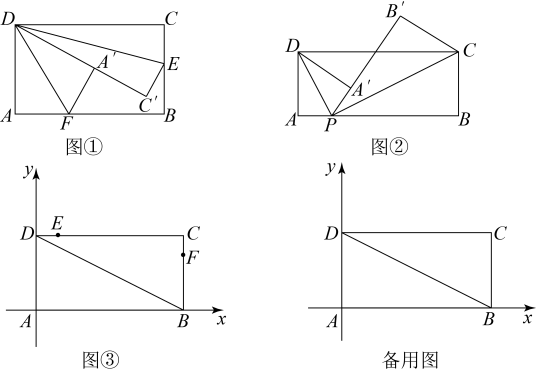
如图①,在矩形的边
上找一点E,将矩形沿直线
折叠,点C的对应点为
, 再在
上找一点F,将矩形沿直线
折叠,使点A的对应点
落在
上则
.
如图②在矩形中,
,
, 点P是矩形
边
上一点,连接
, 将
、
分别沿
翻折,得到
、
, 当P、
、
三点共线时,则称P为
边上的“优叠点”,求此时
的长度.
如图③,矩形位于平面直角坐标系中,
,
. 点A在标原点,B,D分别在x轴与y轴上,点E和点F分别是
和
边上的动点,运动过程中始终保持
. 当点P是
边上唯一的“优叠点”时,连接
交
于点M,连接
交
于点N,请问
是否能取得最大值?如果能,请确定此时点M的位置(即求出点M的坐标)及四边形
的面积,若不能,请说明理由.