-
1.
(2023·坪山模拟)
课本呈现:如图1,在射门游戏中,球员射中球门的难易程度与他所处的位置 对球门
对球门 的张角(
的张角(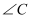 )有关.当球员在
)有关.当球员在 ,
,  处射门时,则有张角
处射门时,则有张角 . 某数学小组由此得到启发,探究当球员在球门
. 某数学小组由此得到启发,探究当球员在球门 同侧的直线
同侧的直线 射门时的最大张角.
射门时的最大张角.
问题探究:
-
(1)
如图2,小明探究发现,若过

、

两点的动圆与直线

相交于点

、

, 当球员在

处射门时,则有

.

小明证明过程如下:
设直线 交圆于点
交圆于点 , 连接
, 连接 , 则
, 则
∵

∴

∴
-
-
(2)
如图3,小红继续探究发现,若过

、

两点的动圆与直线

相切于点

, 当球员在

处射门时,则有

, 你同意吗?请你说明理由.

-
-
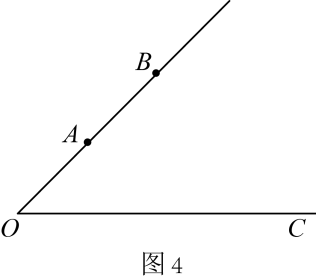
(3)
问题应用:如图4,若

,

米,

是中点,球员在射线

上的

点射门时的最大张角为

, 则

的长度为
米.
-
-
(4)
问题迁移:如图5,在射门游戏中球门

,

是球场边线,

,

是直角,

. 若球员沿

带球前进,记足球所在的位置为点

, 求

的最大度数.(参考数据:

,

,

,

,

. )

-

微信扫码预览、分享更方便


交圆于点
, 连接
, 则


