广东省深圳市坪山区2023年中考二模数学试题（5月）

更新时间：2024-07-14 浏览次数：118 类型：中考模拟

一、单选题

1. (2023·坪山模拟) 在实数3， $\text{[math]}$ ， -1，0中，最小的数是（）

A . 3 B . $\text{[math]}$ C . -1 D . 0

答案解析收藏纠错 + 选题
2. (2023八下·西安期末) 下列数学曲线中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·坪山模拟) 将两本相同的书进行叠放，得到如图所示的几何体，则它的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023·坪山模拟) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·坪山模拟) 爱好运动的小颖同学利用“微信运动”这一公众号，连续记录了8天每天的步数（单位：万步）分别为：1.6，1.3， 1.4，1.7，1.4，1.4 ，1.8，1.6 ，则这组数据的中位数是（）

A . 1.4 B . 1.5 C . 1.6 D . 1.7

答案解析收藏纠错 + 选题
6. (2023·坪山模拟) 中华人民共和国第十四届人民代表大会第一次会议政府工作报告指出：2023年国内生产总值预期增长目标5%左右，城镇新增就业1200万人左右，将1200万用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023·坪山模拟) 如图，一辆自行车竖直摆放在水平地面上，右边是它的部分示意图，测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 到 $\text{[math]}$ 的距离为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·坪山模拟) 某学校将国家级非物质文化遗产“抖空竹”引入阳光特色大课间．某同学“抖空竹”的一个瞬间如图1所示，若将图1抽象成图2的数学问题： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的大小是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·坪山模拟) 密闭容器内有一定质量的二氧化碳，当容器的体积V（单位： $\text{[math]}$ ）变化时，气体的密度ρ（单位： $\text{[math]}$ ）随之变化．已知密度ρ与体积V是反比例函数关系，它的图像如图所示，当 $\text{[math]}$ 时， $\text{[math]}$ ．根据图像可知，下列说法不正确的是（）

A . ρ与V的函数关系式是 $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时，ρ的变化范围是 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023·坪山模拟) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折，点 $\text{[math]}$ 落在点 $\text{[math]}$ 处，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 8 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024九下·惠阳模拟) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023·坪山模拟) $\text{[math]}$ 是关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的一个根，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023·坪山模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．根据尺规作图痕迹，作射线 $\text{[math]}$ ，与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．当 $\text{[math]}$ 时， $\text{[math]}$ 的长是．

答案解析收藏纠错 + 选题
14. (2023·坪山模拟) 如图，在平面直角坐标系中，菱形 $\text{[math]}$ 在第二象限内，边 $\text{[math]}$ 与 $\text{[math]}$ 轴平行， $\text{[math]}$ 、 $\text{[math]}$ 两点纵坐标分别为3、2，反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 、 $\text{[math]}$ 两点．若菱形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2024九上·南山期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上一点，且 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题

三、解答题

16. (2023·坪山模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2023·坪山模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023·坪山模拟) 国家航天局消息：北京时间2022年12月4日，神舟十四号载人飞船返回舱在东风着陆场成功着陆，标志着神舟十四号载人飞行任务取得圆满成功，某中学科技兴趣小组为了解本校学生对航天科技的关注程度，在该校内进行了随机调查统计，将调查结果分为不关注、关注、比较关注、非常关注四类，回收、整理好全部调查问卷后，得到下列不完整的统计图：
1. （1）此次调查中接受调查的人数为人；
2. （2）补全图1条形统计图；
3. （3）该校共有900人，根据调查结果估计该校“关注”，“比较关注”及“非常关注”航天科技的人数共人；
4. （4）该校九年一班非常关注的学生有 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 四人，随机选取两人去参加学校即将举办的航天知识竞赛，则恰好抽到 $\text{[math]}$ 、 $\text{[math]}$ 两位同学的概率为．
答案解析收藏纠错 + 选题
19. (2023·坪山模拟) 某文具店准备购甲、乙两种水笔进行销售，每支进价和利润如表：

甲水笔

乙水笔

每支进价（元）

$\text{[math]}$

$\text{[math]}$

每支利润（元）

2

3

已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等．
1. （1）求甲，乙两种水笔每支进价分别为多少元？
2. （2）若该文具店准备购进这两种水笔共300支，考虑顾客需求，要求购进甲种水笔的数量不少于乙种水笔数量的4倍，问该文具店如何进货能使利润最大，最大利润是多少元？
答案解析收藏纠错 + 选题
20. (2023·坪山模拟) 在平面直角坐标系中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，且该抛物线的顶点 $\text{[math]}$ 在直线 $\text{[math]}$ 上．
1. （1）填空： $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）将抛物线 $\text{[math]}$ 沿直线 $\text{[math]}$ 平移，求平移后所得抛物线与 $\text{[math]}$ 轴交点纵坐标的最大值．
答案解析收藏纠错 + 选题
21. (2023·坪山模拟) 课本呈现：如图1，在射门游戏中，球员射中球门的难易程度与他所处的位置 $\text{[math]}$ 对球门 $\text{[math]}$ 的张角（ $\text{[math]}$ ）有关．当球员在 $\text{[math]}$ ， $\text{[math]}$ 处射门时，则有张角 $\text{[math]}$ ．某数学小组由此得到启发，探究当球员在球门 $\text{[math]}$ 同侧的直线 $\text{[math]}$ 射门时的最大张角．
问题探究：
1. （1）如图2，小明探究发现，若过 $\text{[math]}$ 、 $\text{[math]}$ 两点的动圆与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ 、 $\text{[math]}$ ，当球员在 $\text{[math]}$ 处射门时，则有 $\text{[math]}$ ．
  
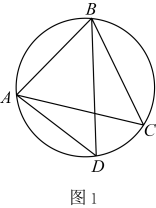
  小明证明过程如下：
  
  设直线 $\text{[math]}$ 交圆于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$
  
  ∵ $\text{[math]}$ $\text{[math]}$
  
  ∴ $\text{[math]}$ $\text{[math]}$
  
  ∴ $\text{[math]}$
2. （2）如图3，小红继续探究发现，若过 $\text{[math]}$ 、 $\text{[math]}$ 两点的动圆与直线 $\text{[math]}$ 相切于点 $\text{[math]}$ ，当球员在 $\text{[math]}$ 处射门时，则有 $\text{[math]}$ ，你同意吗？请你说明理由．
3. （3）问题应用：如图4，若 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ 是中点，球员在射线 $\text{[math]}$ 上的 $\text{[math]}$ 点射门时的最大张角为 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为米．
4. （4）问题迁移：如图5，在射门游戏中球门 $\text{[math]}$ ， $\text{[math]}$ 是球场边线， $\text{[math]}$ ， $\text{[math]}$ 是直角， $\text{[math]}$ ．若球员沿 $\text{[math]}$ 带球前进，记足球所在的位置为点 $\text{[math]}$ ，求 $\text{[math]}$ 的最大度数．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．）
答案解析收藏纠错 + 选题
22. (2023九上·南山期中) 在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的一点，且 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕着点 $\text{[math]}$ 顺时针旋转至 $\text{[math]}$ ，记旋转角为 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ，并以 $\text{[math]}$ 为斜边在其上方作 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）特例探究：如图1，当 $\text{[math]}$ ， $\text{[math]}$ 时，线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系为；
2. （2）问题探究：如图2所示，在旋转的过程中，
  ①（1）中的结论是否依然成立，若成立，请说明理由；
  ②当 $\text{[math]}$ ， $\text{[math]}$ 时，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度；
3. （3）拓展提升：若正方形 $\text{[math]}$ 改为矩形 $\text{[math]}$ ，且 $\text{[math]}$ ，其它条件不变，在旋转的过程中，当 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点共线时，如图3所示，若 $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ 的长度．（用含 $\text{[math]}$ 的式子表示）
答案解析收藏纠错 + 选题