勾股定理的证明
勾股定理揭示了直角三角形三条边之间的数量关系,是数学中最重要的定理之一. 勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.借助于图形的面积研究相关的数量关系,是我国古代数学研究中经常采用的重要方法,它充分显示了古人的卓越智慧.
下面是证明勾股定理的一种思路:
如图,用一个等腰直角三角形(),和两个全等的直角三角形(
)可以拼成一个直角梯形
. 其中
;
, 用两种不同的方法和含有a,b,c的式子表示梯形
的面积,就能完成勾股定理的证明.
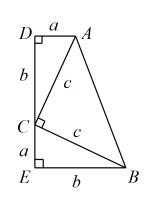
提示:梯形的面积(上底+下底)
高
任务: