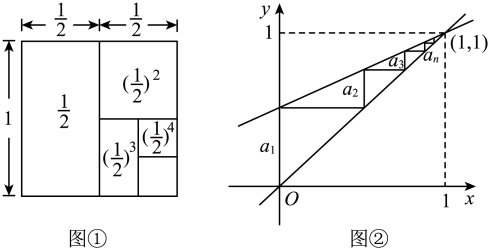
［材料阅读]用数形结合的方法，可以探究的值，其中．例求的值．方法1：借助面积为1的正方形，观察图①可知的结果等于该正方形的面积，即．方法2：借助函数和的图象，观察图②可知的结果等于，，， …，…等各条竖直线段的长度

当前位置：初中数学 / 阅读理解

1. (2023·潍坊) ［材料阅读]
用数形结合的方法，可以探究 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．
例求 $\text{[math]}$ 的值．
方法1：借助面积为1的正方形，观察图①可知
$\text{[math]}$ 的结果等于该正方形的面积，
即 $\text{[math]}$ ．
方法2：借助函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象，观察图②可知
$\text{[math]}$ 的结果等于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ …等各条竖直线段的长度之和，
即两个函数图象的交点到 $\text{[math]}$ 轴的距离．因为两个函数图象的交点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距为1，
所以， $\text{[math]}$ ．

【实践应用】
1. （1）任务一完善 $\text{[math]}$ 的求值过程．
  方法1：借助面积为2的正方形，观察图③可知 $\text{[math]}$ ．
  方法2：借助函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象，观察图④可知
  因为两个函数图象的交点的坐标为，
  所以， $\text{[math]}$ ．
3. （2）任务二参照上面的过程，选择合适的方法，求 $\text{[math]}$ 的值．
5. （3）任务三用方法2，求 $\text{[math]}$ 的值（结果用 $\text{[math]}$ 表示）．
7. （4）【迁移拓展】
  长宽之比为 $\text{[math]}$ 的矩形是黄金矩形，将黄金矩形依次截去一个正方形后，得到的新矩形仍是黄金矩形．
  观察图⑤，直接写出 $\text{[math]}$ 的值．

微信扫码预览、分享更方便

使用过本题的试卷