如图,直线 ,
, 试说明:
.
解:因为 ,
根据“垂直的定义”,①
所以 .
因为 ,
根据“同位角相等,两直线平行”,②
所以 ,
根据“等量代换”,③
所以 ,
根据“垂直的定义”,④
所以 .


|
定理:三角形的中位线平行于第三边,并且等于第三边的一半. 已知:如图,在
求证: 证明:延长 |
甲、乙两人后续证明的部分思路如下:
甲:如图1,先证明 , 再推理得出四边形
是平行四边形.
乙:如图2,连接 ,
. 先后证明四边形
,
分别是平行四边形.
下列判断正确的是( )

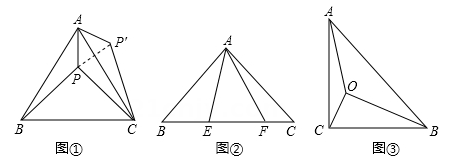
【解决问题】如图2,在直角三角形内部有一动点
,
,
, 连接
,
,
, 若
, 求
的最小值 .

请结合上述材料和已学几何知识解答以下问题:
已知:如图, ,
,
,
,
, 点
是
的中点,那么
的长为.

已知: , 依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,为半径画弧;
步骤2:以B为圆心,为半径画弧,两弧交于点D;
步骤3:连接 , 交
延长线于点E.

下列叙述正确的是.(填写序号)
①垂直平分线段
;②
平分
;③
;④
.
在数学课上,老师提出如下问题:
|
尺规作图:作对角线等于已知线段的菱形. 求作:菱形AMBN,使得其对角线分别等于b和2a. |
小军的作法如下:
| 如图 (1)画一条线段AB等于b; (2)分别以A、B为圆心,大于 在线段AB的上下各作两条弧,两弧相交于P、Q两点; (3)作直线PQ交AB于O点; (4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形. |
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是

托勒密定理:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和. |
如图,正五边形ABCDE内接于 ,
,则对角线BD的长为.

阅读下列材料,并解答以下问题.
完成一件事有k类不同的方案,在第一类方案中有m1个不同的方法,在第二类方案中有m2个不同的方法,…,在第k类方案中有mk个不同的方法,那么,完成这件事共有N=m1+m2+…+mk种不同方法,这是分类加法计数原理.完成一件事有需要分成k个步骤,做第一步有m1种不同方法,做第二步有m2种不同方法,…,做第k步有mk种不同方法,那么完成这件事共有N=m1×m2×…×mk种不同的方法,这就是分步乘法计数原理.
(1)若完成沿图所示的街道从A点出发向B点行进这件事(规定:必须向北或向东走),会有种不同的走法.
(2)若完成沿图所示的街道从A点出发向B点行进,并禁止通过交叉点C这件事(规定:必须向北或向东走),有 种不同的走法.

根据对材料的理解解决以下问题∶

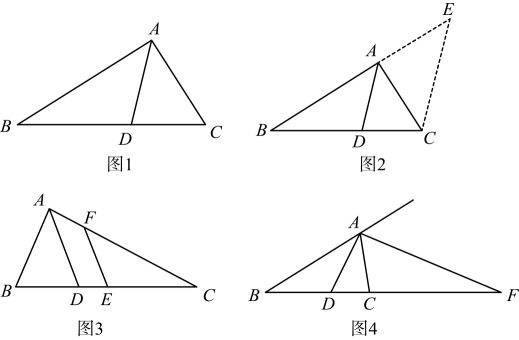
材料:三角形的内角平分线定理:
如图1,在中,
平分
, 交
于点
, 则
.
下面是这个定理的部分证明过程.
证明:如图2,过作
, 交
的延长线于点
.
①找出、
、
、
这四条线段的比例关系,并证明;
②若 ,
, 求
的长.
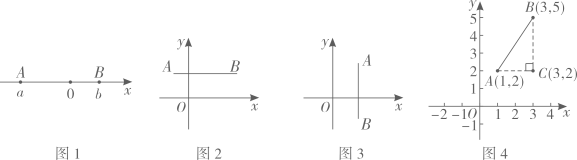
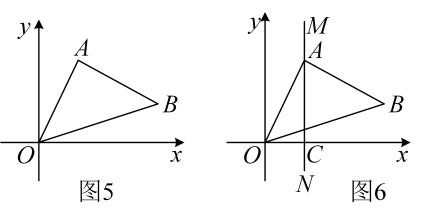
如图1,若点在点
的右侧,则
, 类似的,在平面直角坐标系xOy中,点
的坐标为
, 点
的坐标为
,
如图2,若轴,则
.
如图3,若轴,则
.
如图4,例如 , 则
.
请根据以上阅读材料,解决下面的问题:
小明遇到一个问题:如图1,在▱ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G . 如果=3,求
的值.他的做法是:过点E作EH∥AB交BG于点H , 那么可以得到△BAF∽△HEF . 请回答:

如图2,在四边形ABCD中,DC∥AB , 点E是BC延长线上一点,AE和BD相交于点F . 如果=2,
, 求
的值.
材料:等宽的纸条数根.
折法:如图1,将两根等宽的纸条对折,穿插后重叠部分为正方形.

如图2,取一根等宽的纸条打个结,拉紧,重叠部分即为正五边形.
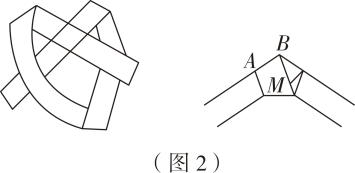
如图3,取两根等宽的纸条折叠穿插,拉紧,可得正六边形.

如图4,把图2的纸条再打一个结,拉紧,重叠部分即为正七边形.

问题:
人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.

如图②,AB与⊙O相切于点A , 当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D , 在上任取一点E , 连接EC , ED , EA , 则∠CED=∠CAD.
任务:
小聪学完了“锐角三角函数”的相关知识后,通过研究发现:如图1,在Rt△ABC中,如果∠C=90°,∠=30°,BC═a=1,AC=b= , AB=c=2,那么
=
=2.通过上网查阅资料,他又知“sin90°=1”,因此他得到“在含30°角的直角三角形中,存在着
=
=
的关系.
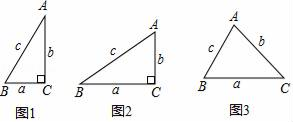
这个关系对于一般三角形还适用吗?为此他做了如下的探究:
如图3,在锐角△ABC中,BC=a,AC=b,AB=c,请判断此时“ =
=
”的关系是否成立?并证明你的判断.(提示:过点C作CD⊥AB于D,过点A作AH⊥BC,再结合定义或其它方法证明).
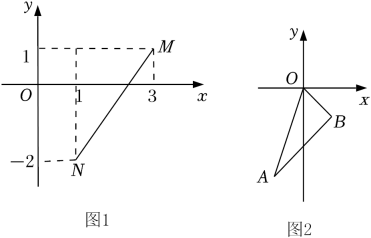
【材料阅读】平面内两点M(x1 , y1),N(x2 , y2),则由勾股定理可得,这两点间的距离MN= .
例如.如图1,M(3,1),N(1,-2),则 .
【直接应用】
 图①
图①
如图②,在中,
, 点
为
内一点,连接
, 且
, 直接写出
的值.
 图②
图②
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.
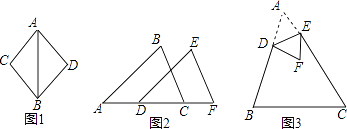
用数形结合的方法,可以探究的值,其中
.
例求的值.
方法1:借助面积为1的正方形,观察图①可知
的结果等于该正方形的面积,
即 .
方法2:借助函数和
的图象,观察图②可知
的结果等于
,
,
, …,
…等各条竖直线段的长度之和,
即两个函数图象的交点到轴的距离.因为两个函数图象的交点
到
轴的距为1,
所以, .
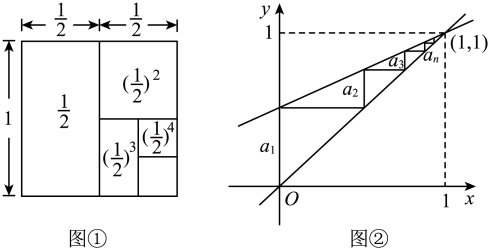


【实践应用】
方法1:借助面积为2的正方形,观察图③可知.
方法2:借助函数和
的图象,观察图④可知
因为两个函数图象的交点的坐标为,
所以,.
长宽之比为的矩形是黄金矩形,将黄金矩形依次截去一个正方形后,得到的新矩形仍是黄金矩形.
观察图⑤,直接写出的值.
如图2,是线段
上的一动点(不与点
,
重合),点
,
分别是线段
,
的中点,以
,
,
为边分别在
的同侧作等边三角形
,
,
, 连接
和
.
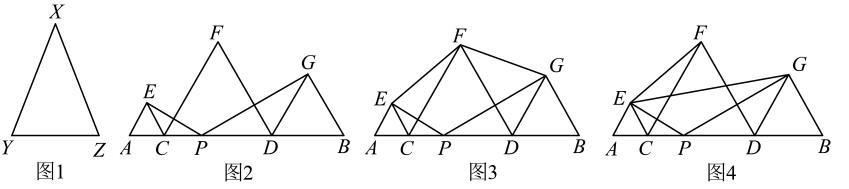
②;
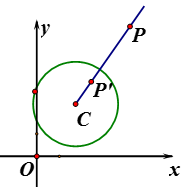
根据上述材料,请你解决以下问题:
①在点 中存在关于⊙O的发散点的是点;其对应发散点的坐标是;
②点P在直线 上,若点P关于⊙O的发散点P′存在,且点P′不在x轴上,求点P的横坐标m的取值范围