山东省潍坊市2023年中考数学真题

更新时间：2023-11-27 浏览次数：283 类型：中考真卷

一、单选题

1. 在实数1，－1，0， $\text{[math]}$ 中，最大的数是（）

A . 1 B . －1 C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列图形由正多边形和圆弧组成，其中既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024九下·黄石月考) 实数a ， b ， c在数轴上对应的点如图所示，下列判断正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·湖南模拟) 在我国古代建筑中经常使用榫卯构件，如图是某种榫卯构件的示意图，其中，卯的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. 如图，在直角坐标系中，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于A ， B两点，下列结论正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·潍坊) 如图，在直角坐标系中，菱形 $\text{[math]}$ 的顶点A的坐标为 $\text{[math]}$ ， $\text{[math]}$ ．将菱形 $\text{[math]}$ 沿x轴向右平移1个单位长度，再沿y轴向下平移1个单位长度，得到菱形 $\text{[math]}$ ，其中点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题

7. (2023·潍坊) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·潍坊) 下列命题正确的是（）

A . 在一个三角形中至少有两个锐角 B . 在圆中，垂直于弦的直径平分弦 C . 如果两个角互余，那么它们的补角也互余 D . 两条直线被第三条直线所截，同位角一定相等

答案解析收藏纠错 + 选题
9. (2023·潍坊) 已知抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ ，则下列结论正确的是（）

A . 拋物线的开口向下 B . 拋物线的对称轴是 $\text{[math]}$ C . 拋物线与 $\text{[math]}$ 轴有两个交点 D . 当 $\text{[math]}$ 时，关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有实根

答案解析收藏纠错 + 选题
10. (2023·潍坊) 发动机的曲柄连杆将直线运动转化为圆周运动，图①是发动机的实物剖面图，图②是其示意图．图②中，点A在直线l上往复运动，推动点B做圆周运动形成 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 表示曲柄连杆的两直杆，点C、D是直线l与 $\text{[math]}$ 的交点；当点A运动到E时，点B到达C；当点A运动到F时，点B到达D ．若 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 当 $\text{[math]}$ 与 $\text{[math]}$ 相切时， $\text{[math]}$ D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

11. (2024八下·博山期末) 从 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 中任意选择两个数，分别填在算式 $\text{[math]}$ 里面的“□”与“○”中，计算该算式的结果是．（只需写出一种结果）

答案解析收藏纠错 + 选题
12. 用与教材中相同型号的计算器，依次按键，显示结果为．借助显示结果，可以将一元二次方程 $\text{[math]}$ 的正数解近似表示为．（精确到 $\text{[math]}$ ）

答案解析收藏纠错 + 选题
13. (2023·潍坊) 投掷两枚骰子，朝上一面的点数之和为7的概率是．

答案解析收藏纠错 + 选题
14. (2023·潍坊) 在《数书九章》（宋·秦九韶）中记载了一个测量塔高的问题：如图所示， $\text{[math]}$ 表示塔的高度， $\text{[math]}$ 表示竹竿顶端到地面的高度， $\text{[math]}$ 表示人眼到地面的高度， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一平面内，点A、C、E在一条水平直线上．已知 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，人从点F远眺塔顶B ，视线恰好经过竹竿的顶端D ，可求出塔的高度．根据以上信息，塔的高度为米．

答案解析收藏纠错 + 选题

四、解答题

15. (2023·潍坊)
1. （1）化简： $\text{[math]}$
2. （2）利用数轴，确定不等式组 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
16. (2023·潍坊) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，重足为点E ，过点E作 $\text{[math]}$ 、交 $\text{[math]}$ 于点F ， G为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. 如图，l是南北方向的海岸线，码头A与灯塔B相距24千米，海岛C位于码头A北偏东 $\text{[math]}$ 方向．一艘勘测船从海岛C沿北偏西 $\text{[math]}$ 方向往灯塔B行驶，沿线勘测石油资源，勘测发现位于码头A北偏东 $\text{[math]}$ 方向的D处石油资源丰富．若规划修建从D处到海岸线的输油管道，则输油管道的最短长度是多少千米？（结果保留根号）

答案解析收藏纠错 + 选题
18. (2023·潍坊) 为研究某种化学试剂的挥发情况，某研究团队在两种不同的场景下做对比实验，收集了该试剂挥发过程中剩余质量y（克）随时间x（分钟）变化的数据（ $\text{[math]}$ ），并分别绘制在直角坐标系中，如下图所示．
1. （1）从 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，选择适当的函数模型分别模拟两种场景下 $\text{[math]}$ 随 $\text{[math]}$ 变化的函数关系，并求出相应的函数表达式；
2. （2）查阅文献可知，该化学试剂发挥作用的最低质量为3克．在上述实验中，该化学试剂在哪种场景下发挥作用的时间更长？
答案解析收藏纠错 + 选题
19. (2023·潍坊) 某中学积极推进校园文学创作，倡导每名学生每学期向校报编辑部至少投1篇稿件．学期末，学校对七、八年级的学生投稿情况进行调查．
【数据的收集与整理】
分别从两个年级随机抽取相同数量的学生，统计每人在本学期投稿的篇数，制作了频数分布表．
投稿篇数（篇）
1
2
3
4
5
七年级频数（人）
7
10
15
12
6
八年级频数（人）
2
10
13
21
4
【数据的描述与分析】
1. （1）求扇形统计图中圆心角 $\text{[math]}$ 的度数，并补全频数直方图．
2. （2）根据频数分布表分别计算有关统计量：
  统计量
  中位数
  众数
  平均数
  方差
  七年级
  3
  3
  $\text{[math]}$
  1.48
  八年级
  m
  n
  3.3
  1.01
  直接写出表格中m、n的值，并求出 $\text{[math]}$ ．
3. （3）【数据的应用与评价】
  从中位数、众数、平均数、方差中，任选两个统计量，对七、八年级学生的投稿情况进行比较，并做出评价．
答案解析收藏纠错 + 选题
20. (2023·潍坊) 工匠师傅准备从六边形的铁皮 $\text{[math]}$ 中，裁出一块矩形铁皮制作工件，如图所示．经测量， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 之间的距离为2米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ ， $\text{[math]}$ ． $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是工匠师傅画出的裁剪虚线．当 $\text{[math]}$ 的长度为多少时，矩形铁皮 $\text{[math]}$ 的面积最大，最大面积是多少？

答案解析收藏纠错 + 选题
21. (2023·潍坊) 如图，正方形 $\text{[math]}$ 内接于 $\text{[math]}$ ，在 $\text{[math]}$ 上取一点E ，连接 $\text{[math]}$ ， $\text{[math]}$ ．过点A作 $\text{[math]}$ ，交 $\text{[math]}$ 于点G ，交 $\text{[math]}$ 于点F ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求阴影部分的面积．
答案解析收藏纠错 + 选题
22. (2023·潍坊) ［材料阅读]
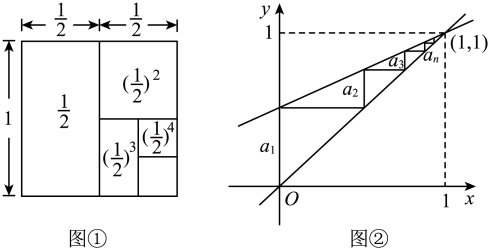
用数形结合的方法，可以探究 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．
例求 $\text{[math]}$ 的值．
方法1：借助面积为1的正方形，观察图①可知
$\text{[math]}$ 的结果等于该正方形的面积，
即 $\text{[math]}$ ．
方法2：借助函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象，观察图②可知
$\text{[math]}$ 的结果等于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ …等各条竖直线段的长度之和，
即两个函数图象的交点到 $\text{[math]}$ 轴的距离．因为两个函数图象的交点 $\text{[math]}$ 到 $\text{[math]}$ 轴的距为1，
所以， $\text{[math]}$ ．

【实践应用】
1. （1）任务一完善 $\text{[math]}$ 的求值过程．
  方法1：借助面积为2的正方形，观察图③可知 $\text{[math]}$ ．
  方法2：借助函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象，观察图④可知
  因为两个函数图象的交点的坐标为，
  所以， $\text{[math]}$ ．
2. （2）任务二参照上面的过程，选择合适的方法，求 $\text{[math]}$ 的值．
3. （3）任务三用方法2，求 $\text{[math]}$ 的值（结果用 $\text{[math]}$ 表示）．
4. （4）【迁移拓展】
  长宽之比为 $\text{[math]}$ 的矩形是黄金矩形，将黄金矩形依次截去一个正方形后，得到的新矩形仍是黄金矩形．
  观察图⑤，直接写出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题