1. (2023八上·浙江期中) 如图①，在△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重复部分……将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，则称∠BAC是△ABC的好玩角．

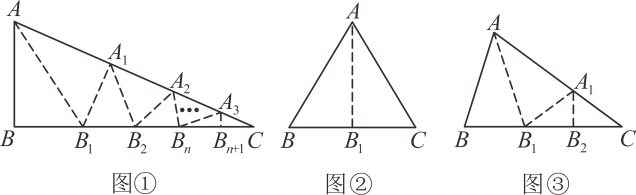
小马展示了确定∠BAC是△ABC的好玩角的两种情形．

情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；

情形二：如图③，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，此时点B₁与点C重合．

1. （1） 探究发现：

   在△ABC中，∠B=66°，∠B>∠C，经过两次折叠，∠BAC是△ABC的好玩角，求∠C的度数．

3. （2） 小马经过三次折叠发现了∠BAC是△ABC的好玩角，请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系为．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好玩角，则∠B与∠C(不妨设∠B>∠C)之间的等量关系为．
5. （3） 应用提升：

   小马找到一个三角形，三个角分别为20°，60°，100°，发现60°和100的两个角都是此三角形的好玩角．请你完成，如果一个三角形的最小角是18°试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好玩角．