精选实践探究题—2024年浙教版数学八（上）期中复习

更新时间：2024-10-21 浏览次数：25 类型：复习试卷

一、全等三角形的性质与判定

1. (2023八上·长兴期末) 【问题背景】
1. （1）如图1，点P是线段 $\text{[math]}$ ， $\text{[math]}$ 的中点，求证： $\text{[math]}$ ；
2. （2）【变式迁移】
  如图2，在等腰 $\text{[math]}$ 中， $\text{[math]}$ 是底边 $\text{[math]}$ 上的高线，点E为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 到点F，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长；
3. （3）【拓展创新】
  如图3，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D为 $\text{[math]}$ 中点，点E在线段 $\text{[math]}$ 上（点E不与点B，点D重合），连接 $\text{[math]}$ ，过点A作 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
2. (2023九下·宁波月考) 如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， D是 $\text{[math]}$ 的中点，点E在线段 $\text{[math]}$ 上，连结 $\text{[math]}$ ，作 $\text{[math]}$ 交直线 $\text{[math]}$ 于点F，连结 $\text{[math]}$ .
1. （1）【初步尝试】
  如图2，当 $\text{[math]}$ ，线段 $\text{[math]}$ 的长度是，线段 $\text{[math]}$ 的长度是.
2. （2）【结论探究】
  如图1，小宁猜想“ $\text{[math]}$ ”，但她未能想出证明思路，小波介绍了添加辅助线的方法，如下表所示，请帮小宁完成证明.
  如图，延长 $\text{[math]}$ 至G，使 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ .
3. （3）【拓展应用】
  如图3，当点E在线段 $\text{[math]}$ 的延长线上时，连结 $\text{[math]}$ ，作 $\text{[math]}$ 交直线 $\text{[math]}$ 于点F，连结 $\text{[math]}$ .请补全图形，并求出当 $\text{[math]}$ 时，线段 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
3. (2024七下·南海月考) 【初步探索】
1. （1）如图1，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， E， F分别是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，探究图中 $\text{[math]}$ 之间的数量关系．小明同学探究此问题的方法是：延长 $\text{[math]}$ 到点G，使 $\text{[math]}$ ．连接 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得出结论，则他的结论应是．
2. （2）【灵活运用】
  如图2，若在四边形 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，上述结论是否仍然成立，并说明理由；
3. （3）【拓展延伸】
  如图3，已知在四边形 $\text{[math]}$ 中， $\text{[math]}$ 若点E在 $\text{[math]}$ 的延长线上，点F在 $\text{[math]}$ 的延长线上，且仍然满足 $\text{[math]}$ ，请写出 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并给出证明过程．
答案解析收藏纠错 + 选题
4. (2023八上·吴兴期中) 在△ABC中，点D在直线AB上，点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180°．
1. （1）【问题解决】
  如图1，若点D在边BA的延长线上，求证：AD+BC=BE；
2. （2）【类比探究】
  如图2，若点D在线段AB上，请直接写出线段AD、BC与BE之间存在怎样的数量关系；
3. （3）【拓展延伸】
  如图3若点D在线段AB的延长线上，请探究线段AD、BC与BE之间的数量关系，并证明．
答案解析收藏纠错 + 选题
5. (2024八上·永嘉月考) 学习了全等三角形后，我们知道中点在平行线之间的题目通常会用到倍长中线构造“8”字型全等的方法，比如在图1，已知 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ 交于点E，若E为 $\text{[math]}$ 中点，则有 $\text{[math]}$ ．请利用以上方法解决下列问题．
问题1：为测量河对岸A点到B点的距离，可借鉴上述方法求值：过点B画直线 $\text{[math]}$ ，并在直线 $\text{[math]}$ 上依次取C点和D点，使得 $\text{[math]}$ ， $\text{[math]}$ ，补全图形，指出测量哪条线段就可知道 $\text{[math]}$ 的长，请加以证明．
问题2：【深入思考】如图3，在 $\text{[math]}$ 中，D是 $\text{[math]}$ 的中点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系并证明．
问题3：如图4，在 $\text{[math]}$ 中， $\text{[math]}$ ， D为 $\text{[math]}$ 中点，连结 $\text{[math]}$ ，作 $\text{[math]}$ 交 $\text{[math]}$ 于点E．已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长______．

答案解析收藏纠错 + 选题
6. (2023八上·浙江期中) 如图①，在△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重复部分……将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，则称∠BAC是△ABC的好玩角．
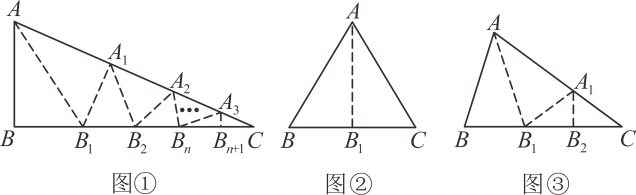
小马展示了确定∠BAC是△ABC的好玩角的两种情形．
情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；
情形二：如图③，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，此时点B₁与点C重合．
1. （1）探究发现：
  在△ABC中，∠B=66°，∠B>∠C，经过两次折叠，∠BAC是△ABC的好玩角，求∠C的度数．
2. （2）小马经过三次折叠发现了∠BAC是△ABC的好玩角，请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系为．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好玩角，则∠B与∠C(不妨设∠B>∠C)之间的等量关系为．
3. （3）应用提升：
  小马找到一个三角形，三个角分别为20°，60°，100°，发现60°和100的两个角都是此三角形的好玩角．请你完成，如果一个三角形的最小角是18°试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好玩角．
答案解析收藏纠错 + 选题
7. (2023八上·临海期中)
1. （1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ，直线l经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E ．证明：DE＝BD+CE ．
2. （2）组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
3. （3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ，求证：I是EG的中点．
答案解析收藏纠错 + 选题

二、特殊三角形

8. (2023八上·余姚月考) 如图
1. （1）【问题发现】如图1，在 $\text{[math]}$ 与 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， B、C、E三点在同一直线上， $\text{[math]}$ ，则 $\text{[math]}$ ．
2. （2）【问题提出】如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ，过点C作 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．
3. （3）【问题解决】如图3，四边形 $\text{[math]}$ 中， $\text{[math]}$ 面积为14且 $\text{[math]}$ 的长为7 ，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
9. (2023八上·兰溪月考) 【问题解决】
如图1，点C为线段AB上一点，∠A＝∠B＝90°，AD＝BC，BE＝AC，连接CD、CE、DE.
1. （1）求证：△ACD≌△BEC.
2. （2）判断△CDE是哪种特殊三角形，并说明理由.
3. （3）【拓展延伸】
  如图2，点C为线段AB上一点，∠A＝∠B＝45°，CD⊥CE.当CD＝CE时，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题

10. (2023八上·温州期中) 为了测量学校旗杆的高度，八(1)班的两个数学研究小组设计了不同的方案，请结合下面表格的信息，完成任务问题．

测量旗杆的高度
测量工具	测量角度的仪器、皮尺等
测量小组	第一小组	第二小组
测量方案示意图
设计方案及测量数据	在地面确定点C，并测得旗杆顶端A的仰角，即∠ACB=45°．	如图1，绳子垂直挂下来时，相比旗杆，测量多出的绳子长度FP为2米．如图2，绳子斜拉直后至末端点P位置，测量点P到地面的距离PD为1米，以及点P到旗杆AB的距离PE为9米．

（1）任务一：判断分析
第一小组要测旗杆AB的高度，只需要测量的长度为线段并说明理由．
（2）任务二：推理计算
利用第二小组获得的数据，求旗杆的高度AB．

答案解析收藏纠错 + 选题

11. (2023八上·杭州期中) 为了测量一条两岸平行的河流的宽度，由于跨河测量困难，所以三个数学研究小组设计了不同的方案，他们在河南岸的点B处测得河北岸的树A恰好在B的正北方向，测量方案如下表：

课题	测量河流宽度
工具	测量角度的仪器，标杆，皮尺等
小组	第一小组	第二小组	第三小组
测量方案	观察者从B点向东走到C点，此时恰好测得： ∠ACB＝45°	观测者从B点向东走到O点，在O点插上一面标杆，继续向东走相同的路程到达C点后，一直向南走到点D ，使得树，标杆，人在同一直线上	观测者从B点出发，沿着南偏西80°的方向走到点C ，此时恰好测得： ∠ACB＝40°
测量示意图

（1）第一小组认为要知道河宽AB ，只需要测量线段_的长度．
（2）第二小组认为只要测得CD就能得到河宽AB ，你认为第二小组的方案可行吗？如果可行，请给出证明；如果不可行，请说明理由．
（3）第三小组测得BC＝35米，请你帮他们求出河宽AB ．

答案解析收藏纠错 + 选题

12. (2024八上·嘉兴期中) 【发现问题】小强在一次学习过程中遇到了下面的问题：如图①，AD是△ABC的中线，若AB＝5，AC＝3，求AD的取值范围．
【探究方法】小强所在的小组通过探究发现，延长AD至点E，使ED＝AD．连接BE，可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到到△ABE中，进而求出AD的取值范围．

方法小结：从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
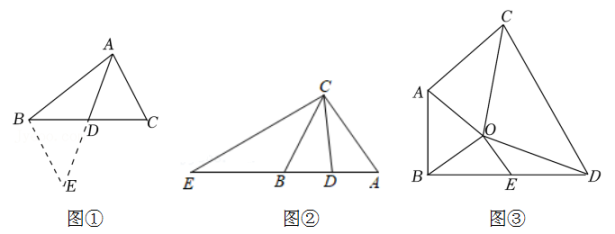
1. （1）请你利用上面解答问题的思路方法，写出求AD的取值范围的过程；
2. （2）【问题解决】
  如图②，CB是△AEC的中线，CD是△ABC的中线，且AB＝AC，下列四个选项中：
  
  A．∠ACD＝∠BCD B．CE＝2CD C．∠BCD＝∠BCE D．CD＝CB
  
  直接写出所有正确选项的序号是．
3. （3）【问题拓展】
  如图③，在△ABO和△CDO中，OA＝OB，OC＝OD，∠AOB与∠COD互补，连接AC、BD，E是BD的中点，求证：OE＝ $\text{[math]}$ AC．
答案解析收藏纠错 + 选题
13. (2023八上·义乌月考) 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形．若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．
1. （1）【理解概念】：
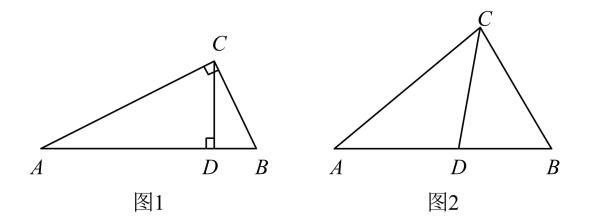
  如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB ，请写出图中两对“等角三角形”．
  ① ．；②．．
2. （2）如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．请你说明CD是△ABC的等角分割线．
3. （3）【应用概念】：
  在△ABC中，若∠A＝40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数．
答案解析收藏纠错 + 选题
14. (2023八上·奉化期中) 如果两个等腰三角形的顶角相等，且顶角的顶点互相重合，如图 $\text{[math]}$ ，等腰 $\text{[math]}$ 与等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，我们把它们构成的这个图形叫做“手拉手模型”．
1. （1）【模型探究】
  如图 $\text{[math]}$ ，线段 $\text{[math]}$ 与线段 $\text{[math]}$ 存在怎样的数量关系？请证明你的结论．
2. （2）【应用模型】
  如图 $\text{[math]}$ ，等腰直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边的中点，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，且 $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的动点，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ ，连结 $\text{[math]}$ ．
  $\text{[math]}$ 如图 $\text{[math]}$ ，当点 $\text{[math]}$ 落在 $\text{[math]}$ 边上时，求 $\text{[math]}$ ．
  $\text{[math]}$ 直接写出在点 $\text{[math]}$ 运动过程中，点 $\text{[math]}$ 和点 $\text{[math]}$ 之间的最短距离．
答案解析收藏纠错 + 选题
15. (2023八上·萧山期中) 如图
1. （1）如图1，把一块三角板（AB＝BC，∠ABC＝90°）放入一个“U”形槽中，使三角形的三个顶点A，B，C分别在槽的两壁及底边上滑动，已知∠D＝∠E＝90°，在滑动过程中；你发现线段AD与BE有什么数量关系？试说明你的结论
2. （2）【变式探究】如图2，在△ABC中，点D、E、F分别在边BC、AB、AC上，若∠B＝∠FDE＝∠C，那么∠BED与∠CDF有何关系，并加以说理；
3. （3）【拓展应用】如图3，在△ABC中，BA=BC，∠B＝45°，点D、F分别是边BC、AB上的动点，且AF=2BD，以DF为腰向右做等腰△DEF，使得DE＝DF，∠EDF＝45°，连接CE.
  ①试判断线段DC、BD、BF之间的数量关系，并说明理由；
  ②如图4，已知AC＝2，点G是AC的中点，连接EA，EG，直接写出EA+EG的最小值．
答案解析收藏纠错 + 选题
16. (2023八上·余姚期中) 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点.
1. （1）特例感知
  等腰直角三角形勾股高三角形(填“是”或“不是”)；
2. （2）如图①， $\text{[math]}$ 为勾股高三角形，其中 $\text{[math]}$ 为勾股顶点， $\text{[math]}$ 是 $\text{[math]}$ 边上的高.若 $\text{[math]}$ ，试求线段 $\text{[math]}$ 的长度.
3. （3）深入探究
  如图②， $\text{[math]}$ 为勾股高三角形，其中 $\text{[math]}$ 为勾股顶点且 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的高.试探究线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并给予证明.
4. （4）推广应用
  如图③，等腰三角形 $\text{[math]}$ 为勾股高三角形，其中 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的高，过点 $\text{[math]}$ 向 $\text{[math]}$ 边引平行线与 $\text{[math]}$ 边交于点 $\text{[math]}$ .若 $\text{[math]}$ ，试求线段 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题
17. (2023八上·柯桥期中)
1. （1）【问题发现】
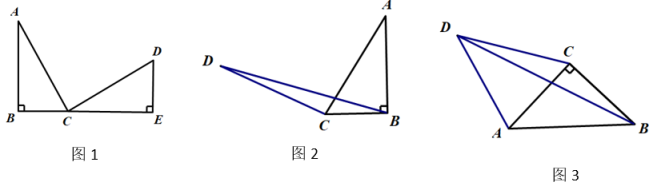
  如图1，在△ABC与△CDE中，∠B=∠E=∠ACD＝90°，AC＝CD，B、C、E三点在同一直线上，AB＝4，ED＝3，则BE=.
2. （2）【问题提出】
  如图2，在Rt△ABC中，∠ABC＝90°，BC＝3，过点C作CD⊥AC，且CD＝AC，求△BCD的面积.
3. （3）【问题解决】
  如图3，四边形ABCD中，∠ABC=∠CAB=∠ADC＝45°，△ACD面积为14且CD的长为7，求△BCD的面积.
答案解析收藏纠错 + 选题

三、一元一次不等式组

18. (2022八上·东阳期中) 小明的数学研学作业单上有这样一道题：已知 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，那么w的取值范围是什么？
【回顾】
小明回顾做过的一道简单的类似题目：已知： $\text{[math]}$ ，设y= $\text{[math]}$ ，那么y的取值范围是               .（请你直接写出答案）
【探究】
小明想：可以将研学单上的复杂问题转化为上面回顾的类似题目.
由 $\text{[math]}$ 得 $\text{[math]}$ ，则 $\text{[math]}$ ，
由 $\text{[math]}$ ， $\text{[math]}$ ，得关于x的一元一次不等式组                ，
解该不等式组得到x的取值范围为                ，
则w的取值范围是               .
【应用】
（1）已知a﹣b＝4，且a＞1，b＜2，设t=a+b，求t的取值范围；
（2）已知a﹣b＝n（n是大于0的常数），且a＞1，b≤1， $\text{[math]}$ 的最大值为          （用含n的代数式表示）；
【拓展】
若 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，设 $\text{[math]}$ ，且m为整数，那么m所有可能的值的和为               .

答案解析收藏纠错 + 选题