浙江省初中名校发展共同体2023-2024学年八年级上学期数...

更新时间：2024-01-09 浏览次数：89 类型：期中考试

一、选择题(本大题共10个小题，每题3分，共30分)

1. (2023八上·浙江期中) 下列图形中，属于轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·浙江期中) 若a<b，则下列结论成立的是（）

A . a+2>b+2 B . -2a<-2b C . 3a>3b D . 1-a>1-b

答案解析收藏纠错 + 选题
3. (2023八上·浙江期中) 在△ABC中，作BC边上的高(图中虚线)，、下列作法正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2023八上·浙江期中) 下列可以作为命题“若x>y，则x²>y²”是假命题的反例是（）

A . x=-2，y=-1 B . x=2，y=-1 C . x=1，y=-2 D . x=2，y=1

答案解析收藏纠错 + 选题
5. (2024七下·耒阳期末) 若等腰三角形的两条边长为2和5，则这个等腰三角形的周长为（）

A . 12 B . 9 C . 12或9 D . 7或15

答案解析收藏纠错 + 选题
6. (2023八上·浙江期中) 如图，在△ABC中，在边AB上取一点P，连结CP，在边CP上取一点Q，连结BQ．若△ACP≌△QBP，∠ACP=23°，则∠CBQ的度数为（）

A . 23° B . 22° C . 30° D . 32°

答案解析收藏纠错 + 选题
7. (2023八上·浙江期中) 在△ABC中，它的三边分别为a，b，c，下列条件：①∠A= $\text{[math]}$ ∠B= $\text{[math]}$ ∠C，②∠A=∠B-∠C，③∠A：∠B：∠C=3：4：5，④a：b：c=2：3： $\text{[math]}$ 其中，能确定△ABC是直角三角形的条件为（）

A . ②③④ B . ①③④ C . ①②④ D . ①②③

答案解析收藏纠错 + 选题
8. (2023八上·浙江期中) 如图，已知钝角三角形ABC，按以下步骤尺规作图，并保留作图痕迹．
步骤1：以C为圆心，CB为半径画弧①；
步骤2：以A为圆心，AB为半径画弧②，交弧①于点D；
步骤3：连结BD，交AC的延长线于点E．
下列叙述正确的是（）

A . BC平分∠ABD B . AB=BD C . AE=BD D . BE=DE

答案解析收藏纠错 + 选题
9. (2023八上·浙江期中) 若关于x的不等式组 $\text{[math]}$ 的整数解共有四个，则a的取值范围是（）

A . 3.5<a≤4 B . 3.5≤a<4 C . 3.5<a<4 D . 3.5≤a≤4

答案解析收藏纠错 + 选题
10. (2023八上·浙江期中) 如图1，以直角三角形的各边分别向外作正方形，再把较小的两个正方形按图2的方式放置在大正方形内，记四边形ABCD面积为S₁ ，四边形CDEG的面积为S₂ ，四边形GFKH的面积为S₃ ，四边形CGHP的面积为S₄ ，若知道图中阴影部分的面积，则一定能求出（）

A . S₁ B . S₂ C . S₃ D . S₄

答案解析收藏纠错 + 选题

二、填空题(本大题有6个小题，每题4分，共24分)

11. (2023八上·浙江期中) 命题“直角三角形的两个锐角互余”的逆命题为．

答案解析收藏纠错 + 选题
12. (2023八上·浙江期中) 如图，B、E、C、F四点在同一直线上，且BE=CF，AC=DF，添加一个条件，使△ABC≌△DEF(写出一个即可)．

答案解析收藏纠错 + 选题
13. (2023八上·浙江期中) 已知三角形的三边长分别为3，5和2x-1，则整数x的最大值为.

答案解析收藏纠错 + 选题
14. (2023八上·浙江期中) 如图，Rt△ABC中，∠C=90°，AC=8，BC=6．有一动点P从点C开始沿C→B→A方向以2cm/s的速度运动到点A后停止运动，当运动时间为秒时，△ACP是等腰三角形．

答案解析收藏纠错 + 选题
15. (2023八上·浙江期中) 如图，在△ABC中，AC=8，BC=15，AB=17，AD平分∠CAB，则△ABD的面积为。

答案解析收藏纠错 + 选题
16. (2023八上·浙江期中) 如图，△ABC为等腰直角三角形，∠ABC=90°，点P在AC的延长线上，且AC=CP=4，将△ABC沿AB方向平移得到△A'B'C'，连结PA'，PC'，则△PA'C'的周长的最小值为.

答案解析收藏纠错 + 选题

三、解答题(本大题有8个小题，第17~19每小题6分，第20，21每小题8分，第22，23每小题10分第24题12分，共66分)

17. (2023八上·浙江期中) 解不等式 $\text{[math]}$ ，并把解在数轴上表示出来．

答案解析收藏纠错 + 选题
18. (2023八上·浙江期中) 如图，AB与CD相交于点O，AB=CD，∠BAD=∠DCB=90°．求证：OB=OD．

答案解析收藏纠错 + 选题
19. (2023八上·浙江期中) 如图，在8×8的方格纸中，△ABC的三个顶点都在格点上，仅用无刻度的直尺，按要求作图．
1. （1）在图1中，画出所有与△ABC全等(不包含△ABC)的△ABP．
2. （2）在图2中，过顶点A画一条直线平分△ABC的面积(不写作法，保留作图痕迹)．
答案解析收藏纠错 + 选题
20. (2023八上·浙江期中) 对于任意两个实数a，b，探究a²+b²与2ab的大小关系：
1. （1）尝试：(用“>”，“=”或“<”填空)
  ①3²+5²2×3×5；
  ②(-3)²+5²2×(-3)×5；
  ③(-3)²+(-3)²2×(-3)×(-3)；
  ④( $\text{[math]}$ )²+( $\text{[math]}$ )²2× $\text{[math]}$ × $\text{[math]}$
2. （2）归纳：对于任意实数a和b，a²+b²与2ab有怎样的大小关系，并说明理由．
答案解析收藏纠错 + 选题
21. (2023八上·浙江期中) 如图，在线段AB的同侧作△PAB和△QAB，PB和QA相交于点O，M、N分别是边AQ、BP的中点，连结PQ，PM，MN，∠APQ=∠ABQ=90°．
1. （1）判断△PMN的形状，并说明理由；
2. （2）当AQ=26，BP=24时，求MN的长．
答案解析收藏纠错 + 选题
22. (2023八上·浙江期中) 污水治理，保护环境，某市治污公司决定购买A，B两种型号污水处理设备共12台，已知A，B两种型号的设备，每台的价格，月处理污水量如表：

A型
B型
价格(万元/台)
a
b
处理污水量(吨/月)
220
180
经调查：购买一台A型设备比购买一台B型设备多3万元，购买1台A型设备比购买3台B型设备少3万元．
1. （1）求a，b的值；
2. （2）经预算：市治污公司购买污水处理设备的资金不超过50万元，你认为该公司有哪几种购买方案
3. （3）在(2)问的条件下，若每月要求处理的污水量不低于2260吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．
答案解析收藏纠错 + 选题
23. (2023八上·浙江期中) 如图①，在△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重复部分……将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，则称∠BAC是△ABC的好玩角．
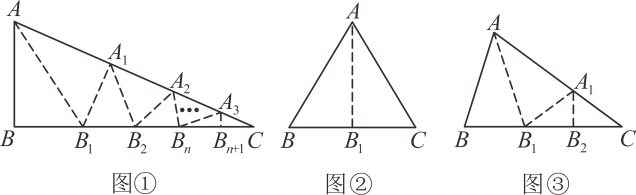
小马展示了确定∠BAC是△ABC的好玩角的两种情形．
情形一：如图②，沿等腰三角形ABC顶角∠BAC的平分线AB₁折叠，点B与点C重合；
情形二：如图③，沿∠BAC的平分线AB₁折叠，剪掉重复部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，此时点B₁与点C重合．
1. （1）探究发现：
  在△ABC中，∠B=66°，∠B>∠C，经过两次折叠，∠BAC是△ABC的好玩角，求∠C的度数．
2. （2）小马经过三次折叠发现了∠BAC是△ABC的好玩角，请探究∠B与∠C(不妨设∠B>∠C)之间的等量关系为．根据以上内容猜想：若经过n次折叠∠BAC是△ABC的好玩角，则∠B与∠C(不妨设∠B>∠C)之间的等量关系为．
3. （3）应用提升：
  小马找到一个三角形，三个角分别为20°，60°，100°，发现60°和100的两个角都是此三角形的好玩角．请你完成，如果一个三角形的最小角是18°试求出三角形另外两个角的度数，使该三角形的三个角均是此三角形的好玩角．
答案解析收藏纠错 + 选题
24. (2023八上·浙江期中) 已知，点M为线段AB的中点，点P为线段AB上一动点，过点P作直线l(不与AB重合)，AE⊥l于．点E，BF⊥I于点F．
1. （1）如图1，当点P与点M重合时，EM与FM有怎样的数量关系，并说明理由；
2. （2）如图2，当点P不与点M重合时，(1)问中的结论是否仍然成立，为什么？
3. （3）在等边△ABC中，点M为AB的中点，点P为AB边上一动点，过点P的直线l∥BC，AE⊥I于点E，BF⊥l于点F，连结BE．
  ①如图3，当AE=BE时，求∠MFE的度数．
  ②如图4，当∠MFE=45°时，探究PM、PB、PE的数量关系，并说明理由．
答案解析收藏纠错 + 选题