1. (2024·深圳模拟) 综合与应用

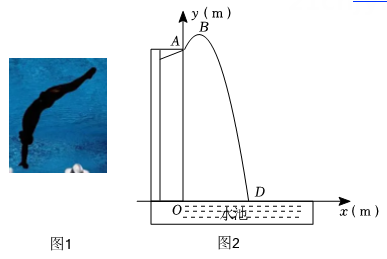
如果将运动员的身体看作一点，则他在跳水过程中运动的轨迹可以看作为抛物线的一部分．建立如图2所示的平面直角坐标系xOy，运动员从点A（0，10）起跳，从起跳到入水的过程中，运动员的竖直高度y （m）与水平距离x （m）满足二次函数的关系.

1. （1） 在平时的训练完成一次跳水动作时，运动员甲的水平距离x与竖直高度y的几组数据如下表：

   水平距离x（m）	0	1	1.5
   竖直高度y（m）	10	10	6.25

   根据上述数据，求出y关于x的关系式；

3. （2） 在（1）的这次训练中，求运动员甲从起点A到入水点的水平距离OD的长；
5. （3） 信息1：记运动员甲起跳后达到最高点B到水面的高度为k（m），从到达到最高点B开始计时，则他到水面的距离h （m）与时间t （s）之间满足h=-5t²+k .

   信息2：已知运动员甲在达到最高点后需要1.6s的时间才能完成极具难度的270C 动作. 

   问题解决：

   ①请通过计算说明，在（1）的这次训练中，运动员甲能否成功完成此动作？

   ②运动员甲进行第二次跳水训练，此时他的竖直高度y（m）与水平距离x （m）的关系为y =ax²-ax+10（a<0），若选手在达到最高点后要顺利完成270C 动作，则a的取值范围是    ▲        .