
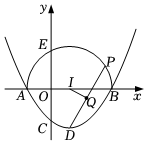
点
在
上;
;
当点
沿半圆从点
运动至点
时,点
运动的路径长为
;
线段
的长可以是
.
其中正确说法的个数为( )

每件售价z(单位:元) | … | 20 | 25 | 30 | … |
销量 | … | 100 | 80 | 60 | … |
其中x , z均为非负整数.商店按照每件甲种玩具利润是每件乙种玩具利润的2倍来确定甲、乙两种玩具的销售单价,且销售单价高于进价.


如果将运动员的身体看作一点,则他在跳水过程中运动的轨迹可以看作为抛物线的一部分.建立如图2所示的平面直角坐标系xOy,运动员从点A(0,10)起跳,从起跳到入水的过程中,运动员的竖直高度y (m)与水平距离x (m)满足二次函数的关系.
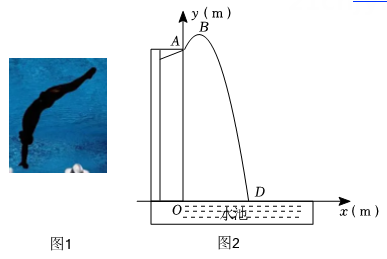
水平距离x(m) | 0 | 1 | 1.5 |
竖直高度y(m) | 10 | 10 | 6.25 |
根据上述数据,求出y关于x的关系式;
信息2:已知运动员甲在达到最高点后需要1.6s的时间才能完成极具难度的270C 动作.
问题解决:
①请通过计算说明,在(1)的这次训练中,运动员甲能否成功完成此动作?
②运动员甲进行第二次跳水训练,此时他的竖直高度y(m)与水平距离x (m)的关系为y =ax2-ax+10(a<0),若选手在达到最高点后要顺利完成270C 动作,则a的取值范围是 ▲ .
| 如何设计跳长绳方案 | ||
| 素材1 | 图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米. |
|
| 素材2 | 某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米. | |
| 问题解决 | ||
| 任务1 | 确定长绳形状 | 在图2中建立合适的直角坐标系,并求出抛物线的函数表达式. |
| 任务2 | 探究站队方式 | 当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶? |
| 任务3 | 拟定位置方案 | 为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围. |