


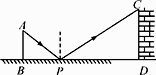
 B .
B .  C .
C .  D .
D . 






按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1 , 依次类推,排在第n位的数称为第n项,记为an .
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
则:
,……
.
∴a2=a1q,a3=a2q=(a1q)q=a1q2 , a4=a3q=(a1q2)q= a1q3 , ……
由此可得:an=(用a1和q的代数式表示)
