江苏省徐州市2018届九年级数学中考一模试卷

更新时间：2018-07-06 浏览次数：629 类型：中考模拟

一、单选题

1. (2018·兴化模拟) 下列图形中，是轴对称图形但不是中心称图形的是（）

A . 等边三角形 B . 正六边形 C . 正方形 D . 圆

答案解析收藏纠错 + 选题
2. (2018·徐州模拟) 下列计算正确的是（）

A . 3⁰=0 B . ﹣|﹣3|=﹣3 C . 3^﹣¹=﹣3 D . $\text{[math]}$ =±3

答案解析收藏纠错 + 选题
3. (2021·乾安模拟) 如图是由四个相同的小正方体组成的立体图形，它的俯视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2018·徐州模拟) 某同学一周中每天体育运动时间（单位：分钟）分别为：35、40、45、40、55、40、48．这组数据的众数、中位数是（）

A . 55、40 B . 40、42.5 C . 40、40 D . 40、45

答案解析收藏纠错 + 选题
5. (2018·徐州模拟) 人体血液中，红细胞的直径约为0.000 007 7m．用科学记数法表示0.000 007 7m是（）

A . 0.77×10^﹣⁵ B . 7.7×10^﹣⁵ C . 7.7×10^﹣⁶ D . 77×10^﹣⁷

答案解析收藏纠错 + 选题
6. (2018·徐州模拟) 袋子里有4个黑球，m个白球，它们除颜色外都相同，经过大量实验，从中任取一个球恰好是白球的频率是0.20，则m的值是（）

A . 1 B . 2 C . 4 D . 16

答案解析收藏纠错 + 选题
7. (2018·徐州模拟)
如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不能得出BE∥DF的是（　　）

A . AE=CF B . BE=DF C . ∠EBF=∠FDE D . ∠BED=∠BFD

答案解析收藏纠错 + 选题
8. (2018·徐州模拟)
如图，点A，B的坐标分别为（1，4）和（4，4），抛物线y=a（x﹣m）²+n的顶点在线段AB上运动（抛物线随顶点一起平移），与x轴交于C、D两点（C在D的左侧），点C的横坐标最小值为﹣3，则点D的横坐标最大值为（）

A . ﹣3 B . 1 C . 5 D . 8

答案解析收藏纠错 + 选题

二、填空题

9. (2018·徐州模拟) 分解因式4ab²﹣9a³=．

答案解析收藏纠错 + 选题
10. (2018·徐州模拟) 若a²﹣2a﹣4=0，则5+4a﹣2a²=．

答案解析收藏纠错 + 选题
11. (2018·徐州模拟) 数轴上的两个数﹣3与a，并且a＞﹣3，它们之间的距离可以表示为．

答案解析收藏纠错 + 选题
12. (2018·徐州模拟) 通过平移把点A（2，﹣3）移到点A′（4，﹣2），按同样的平移方式可将点B（﹣3，1）移到点B′，则点B′的坐标是．

答案解析收藏纠错 + 选题
13. (2023九上·简阳期中) 设x₁、x₂是方程2x²+nx+m=0的两个根，且x₁+x₂=4，x₁x₂=3．则m+n=．

答案解析收藏纠错 + 选题
14. (2018·徐州模拟) 如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=6，BC=8，则EF的长为．

答案解析收藏纠错 + 选题
15. (2018·徐州模拟) 点A（a，b）是函数y=x﹣1与y= $\text{[math]}$ 的交点，则a²b﹣ab²=．

答案解析收藏纠错 + 选题
16. (2018·徐州模拟) 如图，已知AB、AD是⊙O的弦，∠ABO=30°，∠ADO=20°，则∠BAD=．

答案解析收藏纠错 + 选题
17. (2018·徐州模拟) 已知﹣1＜b＜0，0＜a＜1，则代数式a﹣b、a+b、a+b²、a²+b中值最大的是．

答案解析收藏纠错 + 选题
18. (2018·徐州模拟) 如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y= $\text{[math]}$ （x＞0）的图象经过A，B两点．若点A的坐标为（n，1），则k的值为．

答案解析收藏纠错 + 选题

三、解答题

19. (2018·徐州模拟) 计算
1. （1）计算（﹣ $\text{[math]}$ ）^﹣¹+ $\text{[math]}$ ﹣（﹣ $\text{[math]}$ ）⁰
2. （2）计算（ $\text{[math]}$ ）÷ $\text{[math]}$
答案解析收藏纠错 + 选题
20. (2018·徐州模拟) 解答题
1. （1）解不等式组： $\text{[math]}$
2. （2）解方程： $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2021·临清模拟) 某校为更好的开展“春季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳绳、实心球、50m、拔河共四类），并将统计结果绘制成如下不完整的频数分布表（如图所示）
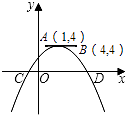
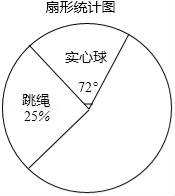
根据以上信息回答下列问题：
最喜爱的趣味运动项目类型频数分布表：
项目类型
频数
频率
跳绳
25
a
实心球
20

50m
b
0.4
拔河

0.15
1. （1）直接写出a=，b=；
2. （2）将图中的扇形统计图补充完整（注明项目、百分比）；
3. （3）若全校共有学生1200名，估计该校最喜爱50m和拔河的学生共约有多少人？
答案解析收藏纠错 + 选题
22. (2018·徐州模拟) 甲、乙、丙三人准备玩传球游戏．规则是：第1次传球从甲开始，甲先将球随机传给乙、丙两人中的一个人，再由接到球的人随机传给其他两人中的一个人…如此反复．
1. （1）若传球1次，球在乙手中的概率为；
2. （2）若传球3次，求球在甲手中的概率（用树状图或列表法求解）．
答案解析收藏纠错 + 选题
23. (2018·徐州模拟) 新房装修后，某居民购买家用品的清单如下表，因污水导致部分信息无法识别，根据下表解决问题：
家居用品名称
单价（元）
数量（个）
金额（元）
垃圾桶
15

鞋架
40

字画
a
2
90
合计
5
185
1. （1）居民购买垃圾桶，鞋架各几个？
2. （2）若居民再次购买字画和垃圾桶两种家居用品共花费150元，则有哪几种不同的购买方案？
答案解析收藏纠错 + 选题
24. (2018·徐州模拟) 如图，在菱形ABCF中，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，EA，延长EA交CD于点G．
1. （1）求证：△ACE≌△CBD；
2. （2）求∠CGE的度数．
答案解析收藏纠错 + 选题
25. (2018·拱墅模拟) 某化工车间发生有害气体泄漏，自泄漏开始到完全控制利用了40min，之后将对泄漏有害气体进行清理，线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x（min）之间的函数关系（0≤x≤40），反比例函数y= $\text{[math]}$ 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x（min）之间的函数关系（40≤x≤？）．根据图象解答下列问题：
1. （1）危险检测表在气体泄漏之初显示的数据是；
2. （2）求反比例函数y= $\text{[math]}$ 的表达式，并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值．
答案解析收藏纠错 + 选题
26. (2018·徐州模拟) 如图，在电线杆CD上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6m的B处安置高为1.5m的测角仪AB，在A处测得电线杆上C处的仰角为30°，求拉线CE的长．（结果保留根号）

答案解析收藏纠错 + 选题
27. (2018·徐州模拟) 在Rt△ABC中，AB=BC=5，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，三角板的两直角边分别交直线AB、BC于E、F两点．
1. （1）如图①，若O为AC的中点，点E、F分别在边AB、BC上．
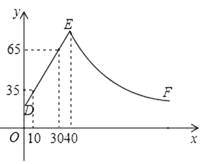
  ①当△OFC是等腰直角三角形时，∠FOC=；
  ②求证：OE=OF；
2. （2）如图②，若AO：AC=1：4时，OE和OF有怎样的数量关系？证明你发现的结论．
答案解析收藏纠错 + 选题
28. (2018·徐州模拟) 在平面直角坐标系中，抛物线y=x²+（k﹣1）x﹣k与直线y=kx+1交于A、B两点，点A在点B的左侧．
1. （1）如图1，当k=1时，直接写出A，B两点的坐标；
2. （2）在（1）的条件下，点P为抛物线上的一个动点，且在直线AB下方，试求出△ABP面积的最大值及此时点P的坐标；
3. （3）如图2，抛物线y=x²+（k﹣1）x﹣k（k＞0）与x轴交于点C、D两点（点C在点D的左侧），是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切？若存在，请求出k的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题