 B .
B .  C .
C .  D .
D . 
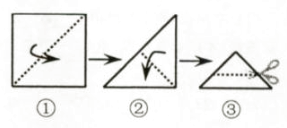
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
收集数据(单位:mm):
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180。
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183。
整理数据:

分析数据:

应用数据:
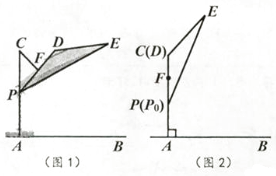
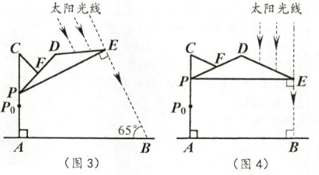
(参考数:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75, ≈1.41,
≈1.73)