江苏省常州市新北区2018届数学中考押题卷

更新时间：2024-07-13 浏览次数：415 类型：中考模拟

一、单选题

1. (2018·新乡模拟) –2的相反数是（）

A . 2 B . $\text{[math]}$ C . –2 D . 以上都不对

答案解析收藏纠错 + 选题
2. (2023七上·景县月考) 据悉，超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（）

A . 5.3×10³ B . 5.3×10⁴ C . 5.3×10⁷ D . 5.3×10⁸

答案解析收藏纠错 + 选题
3. (2018·新北模拟) 下列运算正确的是（）

A . a²+a³=a⁵ B . （a+2b）²=a²+2ab+b² C . a⁶÷a³=a² D . （﹣2a³）²=4a⁶

答案解析收藏纠错 + 选题
4. (2018·新北模拟) 一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形，若小三角形和梯形的面积分别是y和x，则y关于x的函数图象大致是下图中的（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2018·新北模拟) AD与BE是△ABC的角平分线，D，E分别在BC，AC上，若AD=AB，BE=BC，则∠C=（）

A . 69° B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
6. (2018·新北模拟) 已知一次函数y=ax+b的图象经过一、二、三象限，且与x轴交于点（﹣2，0），则不等式ax＞b的解集为（）

A . x＞﹣2 B . x＜﹣2 C . x＞2 D . x＜2

答案解析收藏纠错 + 选题
7. (2023八上·利川期中) 已知实数x，y满足 $\text{[math]}$ ，则以x，y的值为两边长的等腰三角形的周长是（）

A . 30或39 B . 30 C . 39 D . 以上答案均不对

答案解析收藏纠错 + 选题
8. (2024九下·惠城月考) 若关于x的方程mx²﹣mx+2=0有两个相等的实数根，则m的值为（）

A . 0 B . 8 C . 4或8 D . 0或8

答案解析收藏纠错 + 选题
9. (2018·新北模拟) 已知直线y=﹣ $\text{[math]}$ x+3与坐标轴分别交于点A，B，点P在抛物线y=﹣（x﹣ $\text{[math]}$ ）²+4上，能使△ABP为等腰三角形的点P的个数有（）

A . 8个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题

二、填空题

10. (2018·新北模拟) 函数 $\text{[math]}$ 的定义域是．

答案解析收藏纠错 + 选题
11. (2020·杭州模拟) 分解因式（xy﹣1）²﹣（x+y﹣2xy）（2﹣x﹣y）=．

答案解析收藏纠错 + 选题
12. (2018·新北模拟) 某同学进行社会调查，随机抽查了某个地区的20个家庭的收入情况，并绘制了统计图（如图）．
请你根据统计图给出的信息回答：
1. （1）这20个家庭的年平均收入为万元；
2. （2）样本中的中位数是万元，众数是万元；
3. （3）在平均数、中位数两数中，更能反映这个地区家庭的年收入水平．
答案解析收藏纠错 + 选题
13. (2017九上·余姚期中) 如图，在“3×3”网格中，有3个涂成黑色的小方格．若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是．

答案解析收藏纠错 + 选题
14. (2018·新北模拟) 如图，△ABC中，∠BAC=75°，BC=7，△ABC的面积为14，D为 BC边上一动点（不与B，C重合），将△ABD和△ACD分别沿直线AB，AC翻折得到△ABE与△ACF，那么△AEF的面积最小值为．

答案解析收藏纠错 + 选题
15. (2018·新北模拟) 已知x₁和x₂是一元二次方程x²﹣5x﹣k=0的两个实数根，并且x₁和x₂满足不等式 $\text{[math]}$ ＜4，则实数k的取值范围是．

答案解析收藏纠错 + 选题
16. (2018·新北模拟) 如图，在平面直角坐标系中，直线y=﹣3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限内作正方形ABCD，点D在双曲线y= $\text{[math]}$ （k≠0）上，将正方形沿x轴负方向平移a个单位长度后，点C恰好落在该双曲线上，则a的值是．

答案解析收藏纠错 + 选题
17. (2018·新北模拟) 直线y=2x﹣1沿y轴平移3个单位，则平移后直线与y轴的交点坐标为．

答案解析收藏纠错 + 选题

三、解答题

18. 计算：|﹣ $\text{[math]}$ |+（π﹣2017）⁰﹣2sin30°+3^﹣¹ ．

答案解析收藏纠错 + 选题
19. (2018·潮阳模拟) 已知（y﹣z）²+（x﹣y）²+（z﹣x）²=（y+z﹣2x）²+（z+x﹣2y）²+（x+y﹣2z）² ．
求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2018·新北模拟) 解不等式组 $\text{[math]}$ ，并把解集在数轴上表示出来．

答案解析收藏纠错 + 选题
21. (2018·新北模拟) 网络技术的发展对学生学习方式产生巨大的影响，某校为了解学生每周课余利用网络资源进行自主学习的时间，在本校随机抽取若干名学生进行问卷调查，下面是根据调查结果绘制成的不完整的统计图表：
请根据图表中的信息解答下列问题：
组别
学习时间x（h）
频数（人数）
A
0＜x≤1
8
B
1＜x≤2
24
C
2＜x≤3
32
D
3＜x≤4
n
E
4小时以上
4
1. （1）表中的n=，扇形统计图中B组对应的圆心角为°；
2. （2）请补全频数分布直方图；
3. （3）该校准备召开利用网络资源进行自主学习的交流会，计划在E组学生中随机选出两人进行经验介绍，已知E组的四名学生中，七、八年级各有1人，九年级有2人，请用画树状图法或列表法求抽取的两名学生都来自九年级的概率．
答案解析收藏纠错 + 选题
22. (2018·新北模拟) 如图，直线y= $\text{[math]}$ x与反比例函数的图象交于点A（3，a），第一象限内的点B在这个反比例函数图象上，OB与x轴正半轴的夹角为α，且tanα= $\text{[math]}$ ．
1. （1）求反比例函数的解析式；
2. （2）求点B的坐标；
3. （3）求S_△_OAB ．
答案解析收藏纠错 + 选题
23. (2018·新北模拟) 已知，在菱形ABCD中，∠ADC=60°，点H为CD上任意一点（不与C、D重合），过点H作CD的垂线，交BD于点E，连接AE．
1. （1）如图1，线段EH、CH、AE之间的数量关系是；
2. （2）如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时，求证：AE+EH=CH．
答案解析收藏纠错 + 选题
24. (2018·新北模拟) 已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同．甲、乙两人每天共加工35个零件，设甲每天加工x个A型零件．
1. （1）直接写出乙每天加工的零件个数；（用含x的代数式表示）
2. （2）求甲、乙每天各加工零件多少个？
3. （3）根据市场预测，加工A型零件所获得的利润为m元/件（3≤m≤5），加工B型零件所获得的利润每件比A型少1元．求甲、乙每天加工的零件所获得的总利润P（元）与m的函数关系式，并求P的最大值和最小值．
答案解析收藏纠错 + 选题
25. (2018·新北模拟) 如图1，在平面直角坐标系中，一次函数y=﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B．
1. （1）线段AB，BC，AC的长分别为AB=，BC=，AC=；
2. （2）折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2．
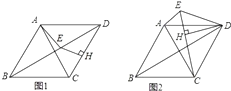
  请从下列A、B两题中任选一题作答，我选择第几题．
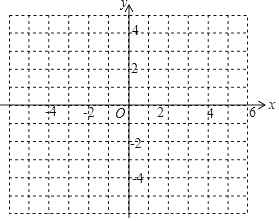
  A：①求线段AD的长；
  ②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由．
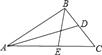
  B：①求线段DE的长；
  ②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
26. (2018·新北模拟) 在△ABC中，AB=AC，∠BAC=α，点P是△ABC内一点，且∠PAC+∠PCA= $\text{[math]}$ ，连接PB，试探究PA、PB、PC满足的等量关系．
1. （1）当α=60°时，将△ABP绕点A逆时针旋转60°得到△ACP′，连接PP′，如图1所示．由△ABP≌△ACP′可以证得△APP′是等边三角形，再由∠PAC+∠PCA=30°可得∠APC的大小为度，进而得到△CPP′是直角三角形，这样可以得到PA、PB、PC满足的等量关系为；
2. （2）如图2，当α=120°时，参考（1）中的方法，探究PA、PB、PC满足的等量关系，并给出证明；
3. （3） PA、PB、PC满足的等量关系为．
答案解析收藏纠错 + 选题
27. (2018·新北模拟) 已知，抛物线y=ax²+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
1. （1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
2. （2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
3. （3） a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
答案解析收藏纠错 + 选题