2015-2016学年江西省南昌市育华学校九年级下学期期中数...

更新时间：2024-07-12 浏览次数：1727 类型：期中考试

一、选择题

1. (2015九下·南昌期中) ﹣2016的相反数是（）

A . ﹣2016 B . 2016 C . ±2016 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2017·凉州模拟) 2015“五一”长假，波月洞景区授待游客约110000人次，将110000用科学记数法表示为（）

A . 11×10⁴ B . 1.1×10⁵ C . 1.1×10⁶ D . 11万

答案解析收藏纠错 + 选题
3. (2022·毕节模拟) 如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）

A . 主视图改变，左视图改变 B . 俯视图不变，左视图不变 C . 俯视图改变，左视图改变 D . 主视图改变，左视图不变

答案解析收藏纠错 + 选题
4. (2015九下·南昌期中) 某年级学生共有246人，其中男生人数y比女生人数x的2倍少2人，则下面所列的方程组中符合题意的有（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2017·凉州模拟) 某兴趣小组10名学生在一次数学测试中的成绩如表（满分150分）
分数（单位：分）
105
130
140
150
人数（单位：人）
2
4
3
1
下列说法中，不正确的是（）

A . 这组数据的众数是130 B . 这组数据的中位数是130 C . 这组数据的平均数是130 D . 这组数据的方差是112.5

答案解析收藏纠错 + 选题
6. (2017·日照模拟)
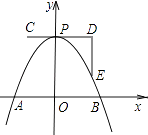
如图，一条抛物线与x轴相交于A，B两点，其顶点P在折线C﹣D﹣E上移动，若点C，D，E的坐标分别为（﹣1，4）、（3，4）、（3，1），点B的横坐标的最小值为1，则点A的横坐标的最大值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

7. (2015九下·南昌期中) 计算：（5a﹣3b）+（9a﹣b）=．

答案解析收藏纠错 + 选题
8. (2015九下·南昌期中) 分解因式：3x²﹣12x+12=．

答案解析收藏纠错 + 选题
9. (2015九下·南昌期中) 已知x^a=3，x^b=5，则x^2a⁺^b=．

答案解析收藏纠错 + 选题
10. (2015九下·南昌期中) 如图，⊙O是正三角形ABC的外接圆，点P在劣弧AB上，∠ABP=22°，则∠BCP的度数为度．

答案解析收藏纠错 + 选题
11. (2015九下·南昌期中) 设a、b是方程x²+x﹣2016=0的两个实数根，则a²+2a+b的值为

答案解析收藏纠错 + 选题
12. (2015九下·南昌期中) 如图，正方形ABCD与正方形AEFG起始时互相重合，现将正方形AEFG绕点A逆时针旋转，设旋转角∠BAE=α（0°＜α＜360°），则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时，α=．

答案解析收藏纠错 + 选题

三、解答题

13. (2015九下·南昌期中) 根据题意解答
1. （1）解不等式组 $\text{[math]}$
2. （2）如图，在正方形ABCD中，点F为CD上一点，BF与AC交于点E，若∠CBF=20°，求∠ADE的度数．
答案解析收藏纠错 + 选题
14. (2015九下·南昌期中) 先化简再求值： $\text{[math]}$ ，其中a=2，b=﹣1．

答案解析收藏纠错 + 选题
15. (2015九下·南昌期中) 直角坐标系中，已知点P（﹣2，﹣1），点T（t，0）是x轴上的一个动点．
1. （1）求点P关于原点的对称点P′的坐标；
2. （2）当t取何值时，△P′TO是等腰三角形？
答案解析收藏纠错 + 选题
16. (2015九下·南昌期中) 如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D、均在小正方形的顶点上，请用无刻度直尺作出以下图形：
①在方格纸中画以AB为一边的菱形ABEF，点E、F在小正方形的顶点上，且菱形ABEF的面积为3；
②在方格纸中画以CD为一边的等腰△CDG，点G在小正方形的顶点上，连接EG，使∠BEG=90°．

答案解析收藏纠错 + 选题
17. (2015九下·南昌期中) 一个不透明的口袋里装有分别标有汉字“幸”、“福”、“聊”、“城”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．
1. （1）若从中任取一个球，球上的汉字刚好是“福”的概率为多少？
2. （2）小颖从中任取一球，记下汉字后放回袋中，然后再从中任取一球，求小颖取出的两个球上汉字恰能组成“幸福”或“聊城”的概率．
答案解析收藏纠错 + 选题
18. (2015九下·南昌期中) 某学校开展课外体育活动，决定开设A：篮球，B：乒乓球，C、踢毽子，D、跳绳四种活动项目，为了解学生最喜欢哪一种活动项目（每人只选取一种），随机抽取了部分学生进行调查，并将调查结果绘成如图统计图，请你结合图中信息解答下列问题．
1. （1）样本中最喜欢A项目的人数所占百分比为，其所在扇形统计图中对应的圆心角度数是度；
2. （2）请把条形统计图补充完整；
3. （3）若该校有学生2000人，请根据样本估计全校最喜欢跳绳的学生人数约是多少？
答案解析收藏纠错 + 选题
19. (2015九下·南昌期中)
如图，一次函数y=kx+b的图像与反比例函数y= $\text{[math]}$ （x＞0）的图像交于点P（n，2），与x轴交于点A（﹣4，0），与y轴交于点C，PB⊥x轴于点B，且AC=BC．
1. （1）求一次函数、反比例函数的解析式；
2. （2）反比例函数图象上是否存在点D，使四边形BCPD为菱形？如果存在，求出点D的坐标；如果不存在，说明理由．
答案解析收藏纠错 + 选题
20. (2015九下·南昌期中) 如图，△ABC中，AB=AC，点D为BC上一点，且AD=DC，过A，B，D三点作⊙O，AE是⊙O的直径，连结DE．
1. （1）求证：AC是⊙O的切线；
2. （2）若sinC= $\text{[math]}$ ，AC=6，求⊙O的直径．
答案解析收藏纠错 + 选题
21. (2015九下·南昌期中) 如图，分别是吊车在吊一物品时的示意图，已知吊车底盘CD的高度为2米，支架BC的长为4米，且与地面成30°角，吊绳AB与支架BC的夹角为75°，吊臂AC与地面成75°角．
1. （1）求证：AB=AC
2. （2）求吊车的吊臂顶端A点距地面的高度是多少米？（保留根号）
答案解析收藏纠错 + 选题
22. (2015九下·南昌期中)
如图，抛物线C₁：y=x²+bx+c经过原点，与x轴的另一个交点为（2，0），将抛物线C₁向右平移m（m＞0）个单位得到抛物线C₂ ， C₂交x轴于A，B两点（点A在点B的左边），交y轴于点C．
1. （1）求抛物线C₁的解析式及顶点坐标；
2. （2）以AC为斜边向上作等腰直角三角形ACD，当点D落在抛物线C₂的对称轴上时，求抛物线C₂的解析式；
3. （3）若抛物线C₂的对称轴存在点P，使△PAC为等边三角形，求m的值．
答案解析收藏纠错 + 选题
23. (2015九下·南昌期中)
在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．
1. （1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；
2. （2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．
  ①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；
  ②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；
  ③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE与PF的数量关系，并给出证明；当BD=m•BP时，请直接写出PE与PF的数量关系．
答案解析收藏纠错 + 选题