浙江省台州市三门城关中学2018-2019学年九年级上学期数...

更新时间：2019-01-16 浏览次数：455 类型：期中考试

一、选择题

1. (2018九上·三门期中) 抛物线y=（x﹣1）²-3的顶点坐标是（）

A . （1，3） B . （﹣1，3） C . （﹣1，﹣3） D . （1，﹣3）

答案解析收藏纠错 + 选题
2. (2018九上·三门期中) 方程x²﹣x=0的解是（）

A . x=0 B . x=1 C . x₁=0，x₂=1 D . x₁=0，x₂=﹣1

答案解析收藏纠错 + 选题
3. (2021九上·福绵期中) 如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则 $\text{[math]}$ 的大小为（）

A . 30° B . 40° C . 50° D . 60°

答案解析收藏纠错 + 选题
4. (2018九上·三门期中) 小丁去看某场电影，只剩下如图所示的六个空座位供他选择，座位号分别为1号、4号、6号、3号、5号和2号．若小丁从中随机抽取一个，则抽到的座位号是偶数的概率是（）

A . $\text{[math]}$ B . C . $\text{[math]}$ D .

答案解析收藏纠错 + 选题
5. (2018九上·三门期中) 如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF⊥AB于F．若AC=2，则OF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
6. (2018九上·三门期中) 抛物线y=2x²向左平移1个单位，再向下平移3个单位，则平移后的解析式为（）

A . y=2（x+1）²﹣3 B . y=2（x+1）²+3 C . y=2（x﹣1）²﹣3 D . y=2（x﹣1）²+3

答案解析收藏纠错 + 选题
7. (2018九上·三门期中) 如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB₁C₁D₁ ，边B₁C₁与CD交于点O，则图中阴影部分的面积是（）

A . $\text{[math]}$ ﹣2﹣ B . $\text{[math]}$ ﹣2+ $\text{[math]}$ C . D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·北京月考) 两个少年在绿茵场上游戏．小红从点A出发沿线段AB运动到点B，小兰从点C出发，以相同的速度沿⊙O逆时针运动一周回到点C，两人的运动路线如图1所示，其中AC $\text{[math]}$ DB．两人同时开始运动，直到都停止运动时游戏结束，其间他们与点C的距离y与时间x（单位：秒）的对应关系如图2所示．则下列说法正确的是（）

A . 小红的运动路程比小兰的长 B . 两人分别在1.09秒和7.49秒的时刻相遇 C . 当小红运动到点D的时候，小兰已经经过了点D D . 在4.84秒时，两人的距离正好等于⊙O的半径

答案解析收藏纠错 + 选题
9. (2018九上·三门期中) 如图，矩形ABCD中，AB=8，BC=6，将矩形ABCD绕点A逆时针旋转得到矩形AEFG，AE，FG分别交射线CD于点PH，连结AH，若P是CH的中点，则△APH的周长为（）

A . 24 B . 20 C . 18 D . 15

答案解析收藏纠错 + 选题
10. (2018九上·三门期中) 如图，⊙O₁的半径为1，正方形ABCD的边长为6，点O₂为正方形ABCD的中心，O₁O₂垂直AB于P点，O₁O₂=8．若将⊙O₁绕点P按顺时针方向旋转360°，在旋转过程中，⊙O₁与正方形ABCD的边只有一个公共点的情况一共出现（）

A . 3次 B . 5次 C . 6次 D . 7次

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·三门期中) 一个扇形的圆心角是120°，面积为3πcm² ，那么这个扇形的半径是．

答案解析收藏纠错 + 选题
12. (2018九上·三门期中) 如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD=°．

答案解析收藏纠错 + 选题
13. (2018九上·三门期中) 正多面体只有五种，分别是正四面体，正六面体，正八面体，正十二面体和正二十面体．如图是一枚质地均匀的正二十面体的骰子，其中的1个面标有“1”，2个面标有“2”，3个面标有“3”，4个面标有“4”，5个面标有“5”，其余的面标有“6”．将这枚骰子随机掷出后，“6”朝上的概率是．

答案解析收藏纠错 + 选题
14. (2018九上·三门期中) 如图，抛物线 $\text{[math]}$ 与直线 $\text{[math]}$ 的两个交点坐标分别为A（﹣2，4），B（1，1），则 $\text{[math]}$ 时 $\text{[math]}$ 的取值范围为．

答案解析收藏纠错 + 选题
15. (2018九上·三门期中) 已知关于x的一元二次方程mx²﹣（m+2）x+2=0有两个不相等的实数根x₁ ， x₂ ，若x₂＜0，且 $\text{[math]}$ ＞﹣1，则整数m的值为．

答案解析收藏纠错 + 选题
16. (2018九上·三门期中) 定义：在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫作图形的γ（a，θ）变换．如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A₁B₁C₁就是△ABC经γ（1，180°）变换后所得的图形．若△ABC经γ（1，180°）变换后得△A₁B₁C₁ ， △A₁B₁C₁经γ（2，180°）变换后得△A₂B₂C₂ ， △A₂B₂C₂经γ（3，180°）变换后得△A₃B₃C₃ ，依此类推……△A_n_﹣1B_n_﹣1C_n_﹣1经γ（n，180°）变换后得△A_nB_nC_n ，则点A₁的坐标是，点A₂₀₂₀的坐标是．

答案解析收藏纠错 + 选题

三、解答题

17. (2018九上·三门期中) 解方程：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2018九上·黄石期中) 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，求线段OE的长．

答案解析收藏纠错 + 选题
19. (2018九上·三门期中) 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．

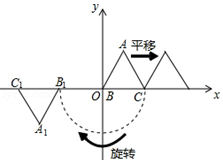
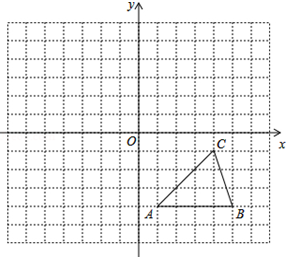
①已知△ABC与△A₁B₁C₁关于原点O对称，请在图中画出△A₁B₁C₁ ，并直接写出C点的对称点C₁的坐标；
② 以原点O为旋转中心，将△ABC顺时针旋转90°得到△A₂B₂C₂ ，请在图中画出△A₂B₂C₂ ，并直接写出C点的对称点C₂的坐标．

答案解析收藏纠错 + 选题
20. (2018九上·三门期中) 在一个不透明的布袋中装有相同的三个小球，其上面分别标注数字﹣1、2、﹣3，现从中任意摸出一个小球，将其上面的数字作为点A的横坐标；将球放回袋中搅匀，再从中任意摸出一个小球，将其上面的数字作为点A的纵坐标．
1. （1）用列表或树状图写出点A坐标的所有可能的结果；
2. （2）求点A在第三象限内的概率.
答案解析收藏纠错 + 选题
21. (2018九上·三门期中) 已知：二次函数y=﹣2x²+4x+m+1，与x轴的公共点为A，B．
1. （1）如果A与B重合，求m的值；
2. （2）横、纵坐标都是整数的点叫做整点：
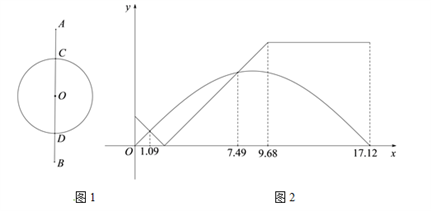
  ①当m=﹣1时，求线段AB上整点的个数；
  
  ②若设抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）整点的个数为n，当1＜n≤8时，结合函数的图象，求m的取值范围．
答案解析收藏纠错 + 选题

22. (2018九上·三门期中) 某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～50千克之间（含20千克和50千克）时，每千克批发价是5元；若超过50千克时，批发的这种蔬菜全部打八折．

（1）根据题意，填写如表：

蔬菜的批发量（千克）	…	25	50	65	80	…
所付的金额（元）	…	125		260		…

（2）此种蔬菜的日销售量y（千克）受零售价x（元/千克）的影响较大，为此该经销商试销一周获得如下数据

零售价x（元/千克）

5

5.5

6

6.5

7

日销售量y（千克）

90

75

60

45

30

根据以上数据求出y与x之间的函数关系式；
（3）若每天批发的蔬菜能够全部销售完，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？此时进货量应为多少？

答案解析收藏纠错 + 选题

23. (2018九上·三门期中) 如图，在平面直角坐标系中，已知△MDC，以CD为直径作⊙O交MD于点A，交MC于点B，连接AB，BC和CD的长分别为2，4，且∠ADC＝45°，求：
1. （1） AB的长和点B的坐标；
2. （2）点M的坐标.
答案解析收藏纠错 + 选题
24. (2018九上·三门期中) 我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．
1. （1） ①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有；
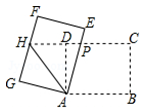
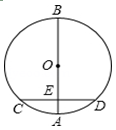
  ②在凸四边形ABCD中，AB=AD且CB≠CD，则该四边形“十字形”．（填“是”或“不是”）
2. （2）如图1，A，B，C，D是半径为1的⊙O上按逆时针方向排列的四个动点，AC与BD交于点E，∠ADB﹣∠CDB=∠ABD﹣∠CBD，当6≤AC²+BD²≤7时，求OE的取值范围；
3. （3）如图2，在平面直角坐标系xOy中，抛物线y=ax²+bx+c（a，b，c为常数，a＞0，c＜0）与x轴交于A，C两点（点A在点C的左侧），B是抛物线与y轴的交点，点D的坐标为（0，﹣ac），记“十字形”ABCD的面积为S，记△AOB，△COD，△AOD，△BOC的面积分别为S₁ ， S₂ ， S₃ ， S₄ ．求同时满足下列三个条件的抛物线的解析式；
  ① $\text{[math]}$ = $\text{[math]}$ ；② $\text{[math]}$ = $\text{[math]}$ ；③“十字形”ABCD的周长为12 $\text{[math]}$ ．
答案解析收藏纠错 + 选题