北京市第四中学2018-2019学年九年级上学期数学期中考试...

更新时间：2019-01-26 浏览次数：411 类型：期中考试

一、选择题

1. (2019九上·北京期中) 抛物线y=-2（x-3）²-4的顶点坐标（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019九上·北京期中) 如图，在Rt△ABC中，∠C=90°，AB=10，AC=8，则sinA等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$

D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019九上·北京期中) 如图，在△ABC中，DE∥BC，DE分别与AB，AC相交于点D，E，若AD=4，DB=2，则DE：BC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$

D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019九上·北京期中) 若A（-4，y₁），B（-1，y₂），C（2，y₃）为二次函数y=-（x+2）²+3的图象上的三点，则y₁ ， y₂ ， y₃小关系是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019九上·北京期中) 如图所示是一个抛物线形桥拱的示意图，在所给出的平面直角坐标系中，当水位在AB位置时，水面宽度为10m，此时水面到桥拱的距离是4m，则抛物线的函数关系式为（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2019九上·北京期中) 如图，已知∠1=∠2，若再增加一个条件不一定能使结论△ADE∽△ABC成立，则这个条件是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2019九上·北京期中) 已知函数y=ax²+bx+c（a≠0）的图象如图，给出下列4个结论：①abc＞0；②b²＞4ac；③4a+2b+c＞0；④2a+b=0．其中正确的有（）个．

A . 1 B . 2 C . 3

D . 4

答案解析收藏纠错 + 选题
8. (2019九上·北京期中) 二次函数y=ax²+bx的图象如图所示，若一元二次方程ax²+bx+m-1=0有两个不相等的实数根，则整数m的最小值为（）

A . 0 B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题

二、填空题

9. (2019九上·北京期中) 在Rt△ABC中，∠C=90°，BC=4，tanA= $\text{[math]}$ ，则AC=

答案解析收藏纠错 + 选题
10. (2019九上·北京期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
11. (2019·广西模拟) 如图是一位同学设计的用手电筒来测量某古城墙高度的示意图．点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB=2米，BP=3米，PD=12米，那么该古城墙的高度CD是米．

答案解析收藏纠错 + 选题
12. (2019九上·北京期中) 抛物线y=-2x²先向右平移1个单位，再向下平移2个单位，所得抛物线的解析式是．

答案解析收藏纠错 + 选题
13. (2019九上·北京期中) 已知二次函数y=x²-x+ $\text{[math]}$ m-1的图象与x轴有公共点，则m的取值范围是．

答案解析收藏纠错 + 选题
14. (2019九上·北京期中) 如图，抛物线y=ax²与直线y=bx+c的两个交点坐标分别为A（-2，4），B（1，1），则关于x的方程ax²-bx-c=0的解为．

答案解析收藏纠错 + 选题
15. (2019九上·北京期中) 已知二次函数y=ax²+bx+c（a，b，c为常数，a≠0），其中自变量x与函数值y之间满足下面的对应关系：

x

…

3

5

7

…

y

…

2.5

2.5

-1.5

…

则a+b+c=．

答案解析收藏纠错 + 选题
16. (2019九上·北京期中) 如图，在△ABC中，AM：MD=4，BD：DC=2：3，则AE：EC=．

答案解析收藏纠错 + 选题

三、计算题

17. (2019九上·北京期中) 若二次函数y=ax²+bx+3的图象经过A（1，0）、B（2，-1）两点，求此二次函数的解析式．

答案解析收藏纠错 + 选题
18. (2019九上·北京期中) 已知：如图，一座商场大楼的顶部竖直立有一个矩形广告牌，小红同学在地面上选择了在一条直线上的三点A（A为楼底）、D、E，她在D处测得广告牌顶端C的仰角为60°，在E两处测得商场大楼楼顶B 的仰角为45°，DE=5米．已知，广告牌的高度BC=2.35米，求这座商场大楼的高度AB（ $\text{[math]}$ 取1.73， $\text{[math]}$ 取1.41，小红的身高不计，结果保留整数）．

答案解析收藏纠错 + 选题

四、解答题

19. (2019九上·北京期中) 求值： $\text{[math]}$ cos²45°-sin30°tan60°+ $\text{[math]}$ sin60°．

答案解析收藏纠错 + 选题
20. (2019九上·北京期中) 已知：如图，在Rt△ABC中，∠ACB=90°，CD是AB边上的高．
1. （1）求证：△ABC∽△CBD；
2. （2）如果AC=4，BC=3，求BD的长．
答案解析收藏纠错 + 选题
21. (2019九上·北京期中) 某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天的销售量y（件）与销售单价x（元）之间的函数关系式是y=-10x+700．当销售单价为多少元时，每天获得的利润最大？并求出利润的最大值．

答案解析收藏纠错 + 选题

22. (2019九上·北京期中) 已知抛物线y₁=x²+2（m+2）x+m-2与x轴交于A，B两点（点A在点B左侧），对称轴为直线x=-1．

（1）求m的值；在坐标系中利用描点法画出此抛物线；

x	…						…
y	…						…

（2）若直线y₂=kx+b过点B且与抛物线交于点P（-2，-3），根据图象直接写出当x取什么值时，y₂≤y₁ ．

答案解析收藏纠错 + 选题

23. (2019九上·北京期中) 在正方形ABCD中，BC=2，点M是边AB的中点，连接DM，DM与AC交于点P．
1. （1）求PD的长；
2. （2）点E在DC上，点F在DP上，且∠DFE=45°．若PF= $\text{[math]}$ ，求CE的长．
答案解析收藏纠错 + 选题
24. (2019九上·北京期中) 已知关于x的一元二次方程mx²+（3m+1）x+3=0．
1. （1）求证：该方程有两个实数根；
2. （2）如果抛物线y=mx²+（3m+1）x+3与x轴交于A、B两个整数点（点A在点B左侧），且m为正整数，求此抛物线的表达式；
3. （3）在（2）的条件下，抛物线y=mx²+（3m+1）x+3与y轴交于点C，点B关于y轴的对称点为D，设此抛物线在-3≤x≤- $\text{[math]}$ 之间的部分为图象G，如果图象G向右平移n（n＞0）个单位长度后与直线CD有公共点，求n的取值范围．
答案解析收藏纠错 + 选题
25. (2019九上·北京期中) 如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．
1. （1）猜想PM与PN的数量关系及位置关系，请直接写出结论；
2. （2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；
3. （3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．
答案解析收藏纠错 + 选题
26. (2019九上·北京期中) 阅读下列材料：
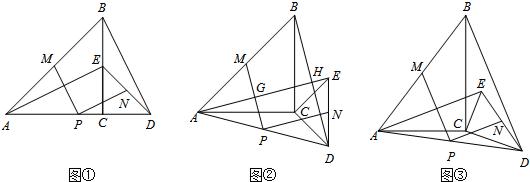
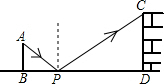
某同学遇到这样一个问题：在平面直角坐标系xOy中，已知直线l：y=-x，点A（1，t）在抛物线y=x²-4x+5上，求点A到直线l的距离d．

如图1，他过点A作AB⊥l于点B，AD∥y轴分别交x轴于点C，交直线l于点 D．他发现OC=CD，∠ADB=45°，可求出AD的长，再利用Rt△ABD求出AB的长，即为点A到直线l的距离d．

请回答：
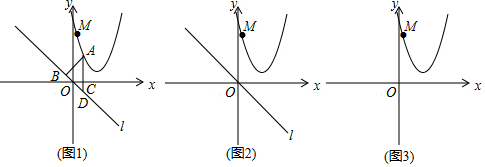
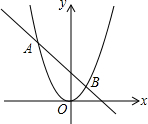
1. （1）图1中，AD=，点A到直线l的距离d=．参考该同学思考问题的方法，解决下列问题：
  在平面直角坐标系xOy中，点M是抛物线y=x²-4x+5上的一动点，设点M到直线l的距离为d．
2. （2）如图2，
  ①l：y=-x，d= $\text{[math]}$ ，则点M的坐标为 ▲ ；
  ②l：y=-x，在点M运动的过程中，求d的最小值。
3. （3）如图3，l：y=2x-7，在点M运动的过程中，d的最小值是．
答案解析收藏纠错 + 选题