2012年浙江省绍兴市中考数学试卷

更新时间：2017-04-25 浏览次数：493 类型：中考真卷

一、选择题

1. (2012·绍兴) 3的相反数是（）

A . 3 B . ﹣3 C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2012·绍兴) 下列运算正确的是（）

A . x+x=x² B . x⁶÷x²=x³ C . x•x³=x⁴ D . （2x²）³=6x⁵

答案解析收藏纠错 + 选题
3. (2012·绍兴) 据科学家估计，地球年龄大约是4 600 000 000年，这个数用科学记数法表示为（）

A . 4.6×10⁸ B . 46×10⁸ C . 4.6×10⁹ D . 0.46×10¹⁰

答案解析收藏纠错 + 选题
4. (2013·河池)
如图所示的几何体，其主视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2012·绍兴) 化简 $\text{[math]}$ 可得（）

A . $\text{[math]}$ B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2012·绍兴)
在如图所示的平面直角坐标系内，画在透明胶片上的▱ABCD，点A的坐标是（0，2）．现将这张胶片平移，使点A落在点A′（5，﹣1）处，则此平移可以是（）

A . 先向右平移5个单位，再向下平移1个单位 B . 先向右平移5个单位，再向下平移3个单位 C . 先向右平移4个单位，再向下平移1个单位 D . 先向右平移4个单位，再向下平移3个单位

答案解析收藏纠错 + 选题
7. (2012·绍兴) 如图，AD为⊙O的直径，作⊙O的内接正三角形ABC，甲、乙两人的作法分别是：
甲：①、作OD的中垂线，交⊙O于B，C两点，
②、连接AB，AC，△ABC即为所求的三角形
乙：①、以D为圆心，OD长为半径作圆弧，交⊙O于B，C两点．
②、连接AB，BC，CA．△ABC即为所求的三角形．
对于甲、乙两人的作法，可判断（）

A . 甲、乙均正确 B . 甲、乙均错误 C . 甲正确、乙错误 D . 甲错误，乙正确

答案解析收藏纠错 + 选题
8. (2012·绍兴) 如图，扇形DOE的半径为3，边长为 $\text{[math]}$ 的菱形OABC的顶点A，C，B分别在OD，OE， $\text{[math]}$ 上，若把扇形DOE围成一个圆锥，则此圆锥的高为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2012·绍兴)
在一条笔直的公路边，有一些树和路灯，每相邻的两盏灯之间有3棵树，相邻的树与树，树与灯间的距离是10m，如图，第一棵树左边5m处有一个路牌，则从此路牌起向右510m～550m之间树与灯的排列顺序是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2012·绍兴) 如图，直角三角形纸片ABC中，AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D重合，折痕与AD交于点P₁；设P₁D的中点为D₁ ，第2次将纸片折叠，使点A与点D₁重合，折痕与AD交于点P₂；设P₂D₁的中点为D₂ ，第3次将纸片折叠，使点A与点D₂重合，折痕与AD交于点P₃；…；设P_n_﹣₁D_n_﹣₂的中点为D_n_﹣₁ ，第n次将纸片折叠，使点A与点D_n_﹣₁重合，折痕与AD交于点P_n（n＞2），则AP₆的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2014·梧州) 分解因式：a³﹣a=．

答案解析收藏纠错 + 选题
12. (2012·绍兴) 教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）之间的关系为y=﹣ $\text{[math]}$ （x﹣4）²+3，由此可知铅球推出的距离是 m．

答案解析收藏纠错 + 选题
13. (2012·绍兴) 箱子中装有4个只有颜色不同的球，其中2个白球，2个红球，4个人依次从箱子中任意摸出一个球，不放回，则第二个人摸出红球且第三个人摸出白球的概率是．

答案解析收藏纠错 + 选题
14. (2012·绍兴) 小明的父母出去散步，从家走了20分钟到一个离家900米的报亭，母亲随即按原速度返回家，父亲在报亭看了10分钟报纸后，用15分钟返回家，则表示父亲、母亲离家距离与时间之间的关系是（只需填序号）．

答案解析收藏纠错 + 选题
15. (2012·绍兴) 如图，在矩形ABCD中，点E、F分别在BC、CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为．

答案解析收藏纠错 + 选题
16. (2012·绍兴)
如图，矩形OABC的两条边在坐标轴上，OA=1，OC=2，现将此矩形向右平移，每次平移1个单位，若第1次平移得到的矩形的边与反比例函数图象有两个交点，它们的纵坐标之差的绝对值为0.6，则第n次（n＞1）平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为（用含n的代数式表示）

答案解析收藏纠错 + 选题

三、解答题

17. (2012·绍兴) 计算下面各题
1. （1）计算：﹣2²+ $\text{[math]}$ ﹣2cos60°+|﹣3|；
2. （2）解不等式组： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2019八上·磴口期中) 如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于 $\text{[math]}$ EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M．
1. （1）若∠ACD=114°，求∠MAB的度数；
2. （2）若CN⊥AM，垂足为N，求证：△ACN≌△MCN．
答案解析收藏纠错 + 选题
19. (2012·绍兴)
如图1，某超市从一楼到二楼的电梯AB的长为16.50米，坡角∠BAC为32°．
1. （1）求一楼与二楼之间的高度BC（精确到0.01米）；
2. （2）电梯每级的水平级宽均是0.25米，如图2．小明跨上电梯时，该电梯以每秒上升2级的高度运行，10秒后他上升了多少米（精确到0.01米）？备用数据：sin32°=0.5299，cos32°=0.8480，tan32°=0.6249．
答案解析收藏纠错 + 选题
20. (2012·绍兴) 一分钟投篮测试规定，得6分以上为合格，得9分以上为优秀，甲、乙两组同学的一次测试成绩如下：
成绩（分）
4
5
6
7
8
9
甲组（人）
1
2
5
2
1
4
乙组（人）
1
1
4
5
2
2
1. （1）请你根据上述统计数据，把下面的图和表补充完整；
  一分钟投篮成绩统计分析表：
  统计量
  平均分
  方差
  中位数
  合格率
  优秀率
  甲组
  2.56
  6
  80.0%
  26.7%
  乙组
  6.8
  1.76
  86.7%
  13.3%
2. （2）下面是小明和小聪的一段对话，请你根据（1）中的表，写出两条支持小聪的观点的理由．
答案解析收藏纠错 + 选题
21. (2012·绍兴) 联想三角形外心的概念，我们可引入如下概念．
定义：到三角形的两个顶点距离相等的点，叫做此三角形的准外心．
举例：如图1，若PA=PB，则点P为△ABC的准外心．
应用：如图2，CD为等边三角形ABC的高，准外心P在高CD上，且PD= $\text{[math]}$ AB，求∠APB的度数．
探究：已知△ABC为直角三角形，斜边BC=5，AB=3，准外心P在AC边上，试探究PA的长．

答案解析收藏纠错 + 选题
22. (2012·绍兴) 小明和同桌小聪在课后复习时，对课本“目标与评定”中的一道思考题，进行了认真的探索．
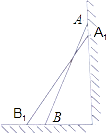
【思考题】如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时B到墙C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？
1. （1）请你将小明对“思考题”的解答补充完整：
  解：设点B将向外移动x米，即BB₁=x，
  则B₁C=x+0.7，A₁C=AC﹣AA₁= $\text{[math]}$ ﹣0.4=2
  而A₁B₁=2.5，在Rt△A₁B₁C中，由 $\text{[math]}$ 得方程，
  解方程得x₁=，x₂=，
  ∴点B将向外移动米．
2. （2）解完“思考题”后，小聪提出了如下两个问题：
  【问题一】在“思考题”中，将“下滑0.4米”改为“下滑0.9米”，那么该题的答案会是0.9米吗？为什么？
  【问题二】在“思考题”中，梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？为什么？
  请你解答小聪提出的这两个问题．
答案解析收藏纠错 + 选题
23. (2012·绍兴) 把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）．
1. （1）如图，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子．
  ①要使折成的长方形盒子的底面积为484cm² ，那么剪掉的正方形的边长为多少？
  ②折成的长方形盒子的侧面积是否有最大值？如果有，求出这个最大值和此时剪掉的正方形的边长；如果没有，说明理由．
2. （2）若在正方形硬纸板的四周剪掉一些矩形（即剪掉的矩形至少有一条边在正方形硬纸板的边上），将剩余部分折成一个有盖的长方形盒子，若折成的一个长方形盒子的表面积为550cm² ，求此时长方形盒子的长、宽、高（只需求出符合要求的一种情况）．
答案解析收藏纠错 + 选题
24. (2012·绍兴)
如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x²﹣4x﹣2经过A，B两点．
1. （1）求A点坐标及线段AB的长；
2. （2）若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒．
  ①当PQ⊥AC时，求t的值；
  ②当PQ∥AC时，对于抛物线对称轴上一点H，∠HOQ＞∠POQ，求点H的纵坐标的取值范围．
答案解析收藏纠错 + 选题