B .
B .  C .
C .  D .
D . 
| 月用水量(吨) | 4 | 5 | 6 | 9 |
| 户数(户) | 3 | 4 | 2 | 1 |
 B .
B . 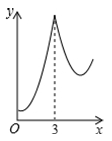 C .
C . 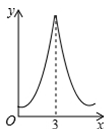 D .
D . 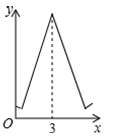

小聪计算这一题的过程如下:
解:原式=(a﹣1)÷ …①
=(a﹣1)• …②
= …③
当a=1,b=1时,原式= …④
以上过程有两处关键性错误,第一次出错在第步(填序号),原因:;
还有第步出错(填序号),原因:.
请你写出此题的正确解答过程.

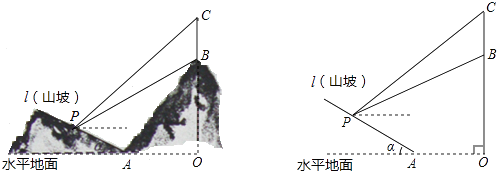
如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)
|
月份(x) |
1月 |
2月 |
3月 |
4月 |
5月 |
6月 |
|
销售量(p) |
3.9万台 |
4.0万台 |
4.1万台 |
4.2万台 |
4.3万台 |
4.4万台 |
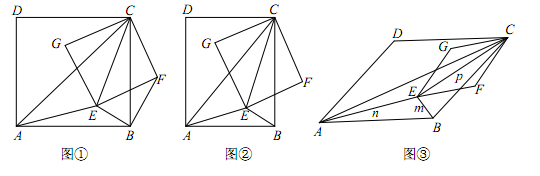
i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;