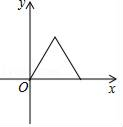浙江省杭州市萧山区2018届数学中考模拟试卷（6月份）

更新时间：2019-04-09 浏览次数：478 类型：中考模拟

一、单选题

1. (2018·萧山模拟) 相反数不大于它本身的数是（）

A . 正数 B . 负数 C . 非正数 D . 非负数

答案解析收藏纠错 + 选题
2. (2018·萧山模拟) 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图，则搭成该几何体的小正方体的个数最少是（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
3. (2018·萧山模拟) 下列计算中，不正确的是（　　）

A . a²•a⁵=a¹⁰ B . a²﹣2ab+b²=（a﹣b）² C . ﹣（a﹣b）=﹣a+b D . ﹣3a+2a=﹣a

答案解析收藏纠错 + 选题
4. (2018·萧山模拟) 如图直线AB，CD，EF被直线a、b所截，若∠1=100°，∠2=100°，∠3=125°，∠4=55°，下列结论错误的是（）

A . EF∥CD∥AB B . C . D .

答案解析收藏纠错 + 选题
5. (2018·萧山模拟) 下图是某学校全体教职工年龄的频数分布直方图（统计中采用“上限不在内”的原则，如年龄为36岁统计在36≤x＜38小组，而不在34≤x＜36小组），根据图形提供的信息，下列说法中错误的是（）

A . 该学校教职工总人数是50人 B . 年龄在40≤x＜42小组的教职工人数占该学校总人数的20% C . 教职工年龄的中位数一定落在40≤x＜42这一组 D . 教职工年龄的众数一定在38≤x＜40这一组

答案解析收藏纠错 + 选题
6. (2018·萧山模拟) 点P的坐标为（﹣3，2），把点P向右平移2个单位后再向下平移5个单位得到点P₁ ，则点P₁的坐标为（）

A . （﹣1，2） B . （﹣5，﹣3） C . （﹣1，﹣3） D . （﹣1，7）

答案解析收藏纠错 + 选题
7. (2018·萧山模拟) 如图，在Rt△ABC中，∠C=90°，点B在CD上，且BD=BA=2AC，则tan∠DAC的值为（）

A . 2+ $\text{[math]}$ B . 2 $\text{[math]}$ C . 3+ $\text{[math]}$ D . 3 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2018·萧山模拟) 在矩形ABCD中，AB=2，AD=4，对角线AC，BD相交于点O，点P是对角线OC上的任意一点（不包括端点），以P为圆心的圆与AD相切，则⊙P与AB的位置关系是（）

A . 相离 B . 相切 C . 相交 D . 不确定

答案解析收藏纠错 + 选题
9. (2021·濠江模拟) 如图，在等边三角形ABC中，点P是BC边上一动点（不与点B，C重合），连接AP，作射线PD，使∠APD=60°，PD交AC于点D，已知AB=a，设CD=y，BP=x，则y与x函数关系的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2021九上·佛山月考) 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念，全班共送1035张照片，如果全班有x名同学，根据题意，列出方程为（）

A . x（x+1）=1035 B . x（x﹣1）=1035×2 C . x（x﹣1）=1035 D . 2x（x+1）=1035

答案解析收藏纠错 + 选题

二、解答题

11. (2018·萧山模拟) 阅读并完成下列各题：
通过学习，同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷．相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．

（例）用简便方法计算995×1005．

解：995×1005

=（1000﹣5）（1000+5）①

=1000²﹣5²②

=999975．
1. （1）例题求解过程中，第②步变形是利用（填乘法公式的名称）；
2. （2）用简便方法计算：
  ①9×11×101×10 001；
  
  ②（2+1）（2²+1）（2⁴+1）…（2³²+1）+1．
答案解析收藏纠错 + 选题
12. (2018·萧山模拟) 某学校为了解该校七年级学生的身高情况，抽样调查了部分同学身高，将所得数据处理后，制成扇形统计图和频数分布直方图（部分）如下（每组只含最低值不含最高值，身高单位：cm，测量时精确到1cm）：
1. （1）请根据所提供的信息补全频数分布直方图；
2. （2）样本的中位数落在（身高值）段中；
3. （3）如果该校七年级共有500名学生，那么估计全校身高在160cm或160cm以上的七年级学生有人；
4. （4）如果上述七年级样本的平均数为157cm，方差为0.8；该校八年级学生身高的平均数为159cm，方差为0.6，那么学生的身高比较整齐．（填“七年级”或“八年级”）
答案解析收藏纠错 + 选题
13. (2018·萧山模拟) 如图，在△ABC中，∠C=90°，AB=10，BC=8，P、Q分别是AB、BC边上的点，且AP=BQ=a （其中0＜a＜8）．
1. （1）若PQ⊥BC，求a的值；
2. （2）若PQ=BQ，把线段CQ绕着点Q旋转180°，试判别点C的对应点C’是否落在线段QB上？请说明理由．
答案解析收藏纠错 + 选题
14. (2018·宁波模拟) 解不等式组 $\text{[math]}$ ；

答案解析收藏纠错 + 选题
15. (2018·萧山模拟) 如图，已知正方形ABCD的边长为 $\text{[math]}$ ，连接AC、BD交于点O，CE平分∠ACD交BD于点E，
1. （1）求DE的长；
2. （2）过点EF作EF⊥CE，交AB于点F，求BF的长；
3. （3）过点E作EG⊥CE，交CD于点G，求DG的长．
答案解析收藏纠错 + 选题
16. (2018·萧山模拟) 在平面直角坐标系xOy中，抛物线y=ax²+4x+c（a≠0）经过点A（3，﹣4）和B（0，2）．
1. （1）求抛物线的表达式和顶点坐标；
2. （2）将抛物线在A、B之间的部分记为图象M（含A、B两点）．将图象M沿直线x=3翻折，得到图象N．若过点C（9，4）的直线y=kx+b与图象M、图象N都相交，且只有两个交点，求b的取值范围．
答案解析收藏纠错 + 选题
17. (2019九下·期中) 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”．
1. （1）概念理解：
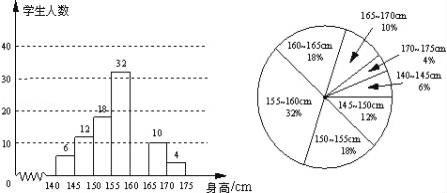
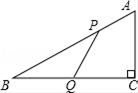
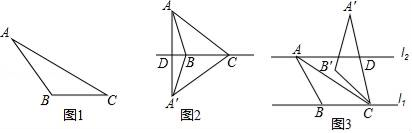
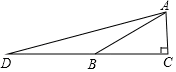
  如图1，在△ABC中，AC=6，BC=3，∠ACB=30°，试判断△ABC是否是”等高底”三角形，请说明理由．
2. （2）问题探究：
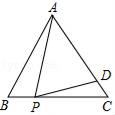
  如图2，△ABC是“等高底”三角形，BC是”等底”，作△ABC关于BC所在直线的对称图形得到△A'BC，连结AA′交直线BC于点D．若点B是△AA′C的重心，求 $\text{[math]}$ 的值．
3. （3）应用拓展：
  如图3，已知l₁∥l₂ ， l₁与l₂之间的距离为2．“等高底”△ABC的“等底”BC在直线l₁上，点A在直线l₂上，有一边的长是BC的 $\text{[math]}$ 倍．将△ABC绕点C按顺时针方向旋转45°得到△A'B'C，A′C所在直线交l₂于点D．求CD的值．
答案解析收藏纠错 + 选题

三、填空题

18. (2018·萧山模拟) 某同学期中考试数学考了100分，则他期末考试数学考100分属于事件．（选填“不可能”“可能”或“必然”）

答案解析收藏纠错 + 选题
19. (2018·萧山模拟) 如图，已知∠1=∠2，∠3=65°，则∠4= .

答案解析收藏纠错 + 选题
20. (2018·萧山模拟) 如图，在⊙O的内接五边形ABCDE中，∠B+∠E=215°，则∠CAD=°．

答案解析收藏纠错 + 选题
21. (2018·萧山模拟) 如图，将直线y=x向下平移b个单位长度后得到直线l，l与反比例函数y= $\text{[math]}$ （x＞0）的图象相交于点A，与x轴相交于点B，则OA²﹣OB²的值为．

答案解析收藏纠错 + 选题
22. (2018·萧山模拟) 已知平行四边形的三个顶点的坐标分别为O（0，0）、A（4，0）、B（2，3），则第四个顶点C的坐标是．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省杭州市萧山区2018届数学中考模拟试卷（6月份）

副标题：

*注意事项：

浙江省杭州市萧山区2018届数学中考模拟试卷（6月份）

试题分析

总体分析

题量分析

难度分析

知识点分析