2018-2019沪科版九年级中期试卷

更新时间：2020-04-26 浏览次数：163 类型：期中考试

一、选择题

1. (2020八下·南通月考) 下列函数中，二次函数是（）

A . y=﹣4x+5 B . y=x（2x﹣3） C . y=（x+4）²﹣x² D . y= $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019九下·期中) 在比例尺是1：40000的地图上，若某条道路长约为5cm，则它的实际长度约为（）

A . 0.2km B . 2km C . 20km D . 200km

答案解析收藏纠错 + 选题
3. (2019九下·期中) 在同一坐标系中，一次函数y=ax+b与二次函数y=ax²﹣b的图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2019九下·期中) 如图，△ABC中，AB=4，BC=6．点D，点E分别是边AB，BC上的两个动点，若按照下列条件将△ABC沿DE剪开，剪下的△BDE与原三角形不相似的是（）

A . ∠BDE=∠C B . DE∥AC C . AD=3，BE=2 D . AD=1，CE=4

答案解析收藏纠错 + 选题
5. (2024九上·拱墅月考) 抛物线y=x²+2x+m﹣1与x轴有两个不同的交点，则m的取值范围是（　　）

A . m＜2 B . m＞2 C . 0＜m≤2 D . m＜﹣2

答案解析收藏纠错 + 选题
6. (2020九上·无锡月考) 如图，l₁∥l₂∥l₃ ，则下列等式错误的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·萧山期中) 若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2019九下·期中) 下列三种方法：①相似三角形对应高的平分线的比等于相似比；②相似三角形对应高的比等于周长比；③周长之比等于1的两个三角形全等，其中正确的说法有（）

A . 1个 B . 2个 C . 3个 D . 0个

答案解析收藏纠错 + 选题
9. (2019九下·锡山期中) 二次函数y=﹣（x﹣1）²+5，当m≤x≤n且mn＜0时，y的最小值为2m，最大值为2n，则m+n的值为（　　）

A . $\text{[math]}$ B . 2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019九下·期中) 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给出以下结论：
①因为a＞0，所以函数y有最大值；②该函数的图象关于直线x=﹣1对称；③当x=﹣2时，函数y的值等于0；④当x=﹣3或x=1时，函数y的值都等于0．其中符合题意结论的个数是（）

A . 4 B . 3 C . 2 D . 1

答案解析收藏纠错 + 选题
11. (2021九上·丰南期中) 函数y=ax²+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）

A . x＜﹣4或x＞2 B . ﹣4＜x＜2 C . x＜0或x＞2 D . 0＜x＜2

答案解析收藏纠错 + 选题
12. (2019九下·期中) 二次函数y=ax²+bx+c（a≠0）的图象经过点（﹣2，0），（x₀ ， 0），1＜x₀＜2，与y轴的负半轴相交，且交点在（0，﹣2）的上方，下列结论：①b＞0；②2a＜b；③2a﹣b﹣1＜0；④2a+c＜0．其中符合题意结论的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题

13. (2019九下·期中) 如图中两三角形相似，则x=．

答案解析收藏纠错 + 选题
14. (2019九下·期中) 如图，四边形ABCD与四边形EFGH位似，位似中心点是O， $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
15. (2019九下·期中) 函数 $\text{[math]}$ 的图象是抛物线，则m=．

答案解析收藏纠错 + 选题
16. (2019九下·期中) 在平面直角坐标系中，点C、D的坐标分别为C（2，3）、D（1，0），现以原点为位似中心，将线段CD放大得到线段AB．若点D的对应点B在x轴上且OB=2，则点C的对应点A的坐标为．

答案解析收藏纠错 + 选题
17. (2019九下·期中) 二次函数y=ax²+bx+c（a，b，c为常数，a≠0）的图象如图所示，下列结论：①abc＜0；②2a+b＜0；③b²﹣4ac=0；④8a+c＜0；⑤a：b：c=﹣1：2：3，其中正确的结论有．

答案解析收藏纠错 + 选题
18. (2019九下·期中) 如图，在矩形ABCD中， $\text{[math]}$ ，∠ADC的平分线交边BC于点E，AH⊥DE于点H，连接CH并延长交边AB于点F，连接AE交CF于点O，给出下列命题：
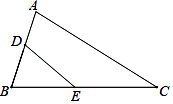
①∠AEB=∠AEH ②DH= $\text{[math]}$ ③ $\text{[math]}$ ④ $\text{[math]}$

其中符合题意命题的序号是（填上所有符合题意命题的序号）.

答案解析收藏纠错 + 选题

三、解答题

19. (2019九下·期中) 已知a：b：c=2：4：5，且2a﹣b+3c=15，求3a+b﹣2c的值．

答案解析收藏纠错 + 选题
20. (2019九下·期中) 如图，已知以点A、
D、E为顶点的三角形与△ABC相似，且AD=3，DE=2.5，AE=4，AC=6，∠AED=∠B，求△ABC的周长．

答案解析收藏纠错 + 选题
21. (2019九下·期中) 在“母亲节”前夕，我市某校学生积极参与“关爱贫困母亲”的活动，他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖，并将所得利润捐给贫困母亲．经试验发现，若每件按24元的价格销售时，每天能卖出36件；若每件按29元的价格销售时，每天能卖出21件．假定每天销售件数y（件）与销售价格x（元/件）满足一个以x为自变量的一次函数．
1. （1）求y与x满足的函数关系式（不要求写出x的取值范围）；
2. （2）在不积压且不考虑其他因素的情况下，销售价格定为多少元时，才能使每天获得的利润P最大？
答案解析收藏纠错 + 选题
22. (2019九下·期中) 如图，在矩形ABCD中，DG⊥AC，垂足为G．
1. （1） △ADG与△AC
  D、△CDG与△CAD相似吗？为什么？
2. （2）若AG=6，CG=12，求矩形ABCD的面积．
答案解析收藏纠错 + 选题
23. (2019九下·期中) 如图，某日的钱塘江观潮信息如表：

按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离（千米）与时间（分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点 $\text{[math]}$ ，点 $\text{[math]}$ 坐标为 $\text{[math]}$ ，曲线 $\text{[math]}$ 可用二次函数 $\text{[math]}$ （ $\text{[math]}$ ，是常数）刻画．
1. （1）求 $\text{[math]}$ 的值，并求出潮头从甲地到乙地的速度；
2. （2） 11：59时，小红骑单车从乙地出发，沿江边公路以0.48千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？
3. （3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为0.48千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度 $\text{[math]}$ ， $\text{[math]}$ 是加速前的速度）
答案解析收藏纠错 + 选题
24. (2019九下·期中) 如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，点P为射线BD，CE的交点．
1. （1）求证：BD=CE；
2. （2）若AB=2，AD=1，把△ADE绕点A旋转，当∠EAC=90°时，求PB的长；
答案解析收藏纠错 + 选题
25. (2019九下·期中) 在平面直角坐标系中，Rt△AOB的位置如图所示，已知∠AOB=90°，AO=BO，点A的坐标为（﹣3，1）．
1. （1）求点B的坐标；
2. （2）求过A、O、B三点的抛物线的解析式；
3. （3）设点P为抛物线上到x轴的距离为1的点，点B关于抛物线的对称轴l的对称点为B₁ ，求点P的坐标和△B₁PB的面积．
答案解析收藏纠错 + 选题
26. (2019九下·期中) 我们定义：如果一个三角形一条边上的高等于这条边，那么这个三角形叫做“等高底”三角形，这条边叫做这个三角形的“等底”．
1. （1）概念理解：
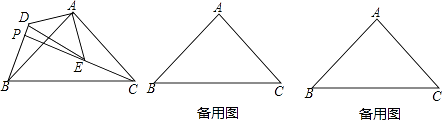
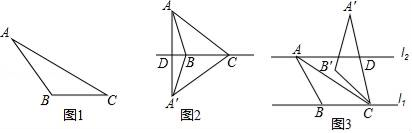
  如图1，在△ABC中，AC=6，BC=3，∠ACB=30°，试判断△ABC是否是”等高底”三角形，请说明理由．
2. （2）问题探究：
  如图2，△ABC是“等高底”三角形，BC是”等底”，作△ABC关于BC所在直线的对称图形得到△A'BC，连结AA′交直线BC于点D．若点B是△AA′C的重心，求 $\text{[math]}$ 的值．
3. （3）应用拓展：
  如图3，已知l₁∥l₂ ， l₁与l₂之间的距离为2．“等高底”△ABC的“等底”BC在直线l₁上，点A在直线l₂上，有一边的长是BC的 $\text{[math]}$ 倍．将△ABC绕点C按顺时针方向旋转45°得到△A'B'C，A′C所在直线交l₂于点D．求CD的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

2018-2019沪科版九年级中期试卷

副标题：

*注意事项：

2018-2019沪科版九年级中期试卷

试题分析

总体分析

题量分析

难度分析

知识点分析