2013年浙江省衢州市中考数学试卷

更新时间：2024-07-12 浏览次数：575 类型：中考真卷

一、选择题

1. (2013·衢州) 比1小2的数是（）

A . 3 B . 1 C . ﹣1 D . ﹣2

答案解析收藏纠错 + 选题
2. (2013·衢州) 下列计算正确的是（）

A . 3a+2b=5ab B . a•a⁴=a⁴ C . a⁶÷a²=a³ D . （﹣a³b）²=a⁶b²

答案解析收藏纠错 + 选题
3. (2013·衢州) 衢州新闻网2月16日讯，2013年春节“黄金周”全市接待游客总数为833100人次．将数833100用科学记数法表示应为（）

A . 0.833×10⁶ B . 83.31×10⁵ C . 8.331×10⁵ D . 8.331×10⁴

答案解析收藏纠错 + 选题
4. (2021·乌鲁木齐模拟) 下面简单几何体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2013·衢州) 若函数y= $\text{[math]}$ 的图象在其所在的每一象限内，函数值y随自变量x的增大而增大，则m的取值范围是（）

A . m＜﹣2 B . m＜0 C . m＞﹣2 D . m＞0

答案解析收藏纠错 + 选题
6. (2013·衢州) 将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（）

A . 3cm B . 6cm C . $\text{[math]}$ cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
7. (2013·衢州) 一次数学测试，某小组五名同学的成绩如表所示（有两个数据被遮盖）．
组员
甲
乙
丙
丁
戊
方差
平均成绩
得分
81
79
■
80
82
■
80
那么被遮盖的两个数据依次是（）

A . 80，2 B . 80， $\text{[math]}$ C . 78，2 D . 78， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2013·衢州)
如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（）（结果精确到0.1m， $\text{[math]}$ ≈1.73）．

A . 3.5m B . 3.6m C . 4.3m D . 5.1m

答案解析收藏纠错 + 选题
9. (2013·衢州) 抛物线y=x²+bx+c的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y=（x﹣1）²﹣4，则b、c的值为（）

A . b=2，c=﹣6 B . b=2，c=0 C . b=﹣6，c=8 D . b=﹣6，c=2

答案解析收藏纠错 + 选题
10. (2013·衢州)
如图，正方形ABCD的边长为4，P为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映y与x的函数关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2013·衢州) 不等式组 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
12. (2013·衢州) 化简： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
13. (2013·衢州) 小芳同学有两根长度为4cm、10cm的木棒，她想钉一个三角形相框，桌上有五根木棒供她选择（如图所示），从中任选一根，能钉成三角形相框的概率是．

答案解析收藏纠错 + 选题
14. (2013·衢州) 如图，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧（ $\text{[math]}$ ）对应的圆心角（∠AOB）为120°，OC的长为2cm，则三角板和量角器重叠部分的面积为．

答案解析收藏纠错 + 选题
15. (2013·衢州) 某果园有100棵橘子树，平均每一棵树结600个橘子．根据经验估计，每多种一棵树，平均每棵树就会少结5个橘子．设果园增种x棵橘子树，果园橘子总个数为y个，则果园里增种棵橘子树，橘子总个数最多．

答案解析收藏纠错 + 选题
16. (2013·衢州) 如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A₁B₁C₁D₁；顺次连结四边形A₁B₁C₁D₁各边中点，可得四边形A₂B₂C₂D₂；顺次连结四边形A₂B₂C₂D₂各边中点，可得四边形A₃B₃C₃D₃；按此规律继续下去…．则四边形A₂B₂C₂D₂的周长是；四边形A₂₀₁₃B₂₀₁₃C₂₀₁₃D₂₀₁₃的周长是．

答案解析收藏纠错 + 选题

三、简答题

17. (2013·衢州) $\text{[math]}$ ﹣2³÷|﹣2|×（﹣7+5）

答案解析收藏纠错 + 选题
18. (2020九上·合浦期中) 如图所示，在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形．
1. （1）用a，b，x表示纸片剩余部分的面积；
2. （2）当a=6，b=4，且剪去部分的面积等于剩余部分的面积时，求正方形的边长．
答案解析收藏纠错 + 选题
19. (2013·衢州) 如图，函数y₁=﹣x+4的图象与函数y₂= $\text{[math]}$ （x＞0）的图象交于A（a，1）、B（1，b）两点．
1. （1）求函数y₂的表达式；
2. （2）观察图象，比较当x＞0时，y₁与y₂的大小．
答案解析收藏纠错 + 选题
20. (2013·衢州) 如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．
1. （1）求证：直线CD是⊙O的切线；
2. （2）若DE=2BC，求AD：OC的值．
答案解析收藏纠错 + 选题
21. (2013·衢州) 据《2012年衢州市国民经济和社会发展统计公报》（2013年2月5日发布），衢州市固定资产投资的相关数据统计图如下：
根据以上信息，解答下列问题：
1. （1）求2012年的固定资产投资增长速度（年增长速度即年增长率）；
2. （2）求2005﹣2012年固定资产投资增长速度这组数据的中位数；
3. （3）求2006年的固定资产投资金额，并补全条形图；
4. （4）如果按照2012年的增长速度，请预测2013年衢州市的固定资产投资金额可达到多少亿元（精确到1亿元）？
答案解析收藏纠错 + 选题
22. (2022·垦利模拟)
1. （1）【提出问题】
  如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
2. （2）【类比探究】
  如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
3. （3）【拓展延伸】
  如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．
答案解析收藏纠错 + 选题
23. (2013·衢州)
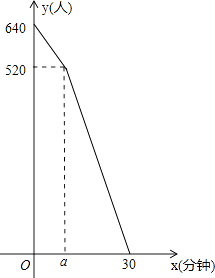
“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．
1. （1）求a的值．
2. （2）求检票到第20分钟时，候车室排队等候检票的旅客人数．
3. （3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？
答案解析收藏纠错 + 选题
24. (2013·衢州)
在平面直角坐标系xOy中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒 $\text{[math]}$ 个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．
1. （1）当点P移动到点D时，求出此时t的值；
2. （2）当t为何值时，△PQB为直角三角形；
3. （3）已知过O、P、Q三点的抛物线解析式为y=﹣ $\text{[math]}$ （x﹣t）²+t（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题