河南省2019届数学中考模试试卷（一)

更新时间：2019-04-23 浏览次数：680 类型：中考模拟

一、单选题

1. (2019·河南模拟) ﹣3的绝对值是（　　）

A . ﹣3 B . 3 C . - D .

答案解析收藏纠错 + 选题
2. (2024九下·绵阳模拟) 中国的陆地面积和领水面积共约9970000km² ， 9970000这个数用科学记数法可表示为（）

A . 9.97×10⁵ B . 99.7×10⁵ C . 9.97×10⁶ D . 0.997×10⁷

答案解析收藏纠错 + 选题
3. (2020·永宁模拟) 如图是由棱长为1的正方体搭成的某几何体三视图，则图中棱长为1的正方体的个数是（）

A . 9 B . 8 C . 7 D . 6

答案解析收藏纠错 + 选题
4. (2019八下·南岸期中) 一次函数y=﹣3x+b和y=kx+1的图象如图所示，其交点为P（3，4），则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2019·河南模拟) 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛，在选拔赛中，每人射击10次，然后从他们的成绩平均数（环）及方差两个因素进行分析，甲、乙、丙的成绩分析如表所示，丁的成绩如图所示．
甲
乙
丙
平均数
7.9
7.9
8.0
方差
3.29
0.49
1.8
根据以上图表信息，参赛选手应选（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
6. (2023·青岛模拟) 如图，四边形ABCD内接于⊙O，F是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接CF并延长交AD的延长线于点E，连接AC，若∠ABC=105°，∠BAC=25°，则∠E的度数为（　　）

A . 45° B . 50° C . 55° D . 60°

答案解析收藏纠错 + 选题
7. (2019·河南模拟) 如图，菱形OABC的一边OA在x轴上，将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置，若OB= $\text{[math]}$ ，∠C=120°，则点B′的坐标为（　　）

A . （3，） B . （3，- ） C . （，） D . （，- ）

答案解析收藏纠错 + 选题
8. (2019·河南模拟)
如图，在▱ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则S_△DEF：S_△AOB的值为（　　）

A . 1：3 B . 1：5 C . 1：6 D . 1：11

答案解析收藏纠错 + 选题
9. (2019·河南模拟) 如图，在平面直角坐标系中，抛物线y= $\text{[math]}$ x²经过平移得到抛物线y=ax²+bx，其对称轴与两段抛物线所围成的阴影部分的面积为 $\text{[math]}$ ，则a、b的值分别为（　　）

A . ， $\text{[math]}$ B . ，﹣ C . ，﹣ $\text{[math]}$ D . ﹣ ， $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019·河南模拟) 在平面直角坐标系中，正方形A₁B₁C₁D₁、D₁ E₁E₂B₂、A₂B₂ C₂D₂、D₂E₃E4B₃…按如图所示的方式放置，其中点B₁在y轴上，点C₁、E₁、E₂、C₂、E₃、E₄、C₃…在x轴上，已知正方形A₁B₁C₁D₁的边长为l，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃…，则正方形A₂₀₁₇B₂₀₁₇C₂₀₁₇ D₂₀₁₇的边长是（　　）

A . （ $\text{[math]}$ ）²⁰¹⁶ B . （ $\text{[math]}$ ）²⁰¹⁷ C . （ $\text{[math]}$ ）²⁰¹⁶ D . （ $\text{[math]}$ ）²⁰¹⁷

答案解析收藏纠错 + 选题

二、填空题

11. (2019·河南模拟) 计算： $\text{[math]}$ +（π﹣2）⁰+（﹣1）²⁰¹⁷=．

答案解析收藏纠错 + 选题
12. (2019·河南模拟) 已知关于x的一元二次方程ax²﹣（a+2）x+2=0有两个不相等的正整数根时，整数a的值是．

答案解析收藏纠错 + 选题
13. (2019·河南模拟) 如图，已知第一象限内的点A在反比例函数y= $\text{[math]}$ 上，第二象限的点B在反比例函数y= $\text{[math]}$ 上，且OA⊥OB，tanA= $\text{[math]}$ ，则k的值为．

答案解析收藏纠错 + 选题
14. (2019·河南模拟) 如图，扇形OAB中，∠AOB=60°，扇形半径为4，点C在 $\text{[math]}$ 上，CD⊥OA，垂足为点D，当△OCD的面积最大时，图中阴影部分的面积为．

答案解析收藏纠错 + 选题
15. (2019·河南模拟) 如图，在矩形ABCD中，AB=5，BC=3，点E为射线BC上一动点，将△ABE沿AE折叠，得到△AB′E．若B′恰好落在射线CD上，则BE的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2019·河南模拟) 先化简，再求值： $\text{[math]}$ ÷ $\text{[math]}$ ，其中m是方程x²＋2x－3＝0的根．

答案解析收藏纠错 + 选题

17. (2019·河南模拟) 在信息快速发展的社会，“信息消费”已成为人们生活的重要组成部分．某高校组织课外小组在郑州市的一个社区随机抽取部分家庭，调查每月用于信息消费的金额，根据数据整理成如图所示的不完整统计表和统计图．已知A，B两组户数频数直方图的高度比为1：5．

月信息消费额分组统计表

组别	消费额（元）
A	10≤x＜100
B	100≤x＜200
C	20≤x＜300
D	300≤x＜400
E	x≥400

请结合图表中相关数据解答下列问题：

（1）这次接受调查的有户；
（2）在扇形统计图中，“E”所对应的圆心角的度数是；
（3）请你补全频数直方图；
（4）若该社区有2000户住户，请估计月信息消费额不少于200元的户数是多少？

答案解析收藏纠错 + 选题

18. (2019·河南模拟) 如图，AB是半圆O的直径，点P是半圆上不与点A、B重合的一个动点，延长BP到点C，使PC=PB，D是AC的中点，连接PD，PO.
1. （1）求证：△CDP≌△POB；
2. （2）填空：
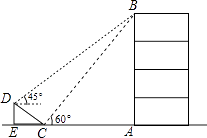
  ①若AB=4，则四边形AOPD的最大面积为；
  
  ②连接OD，当∠PBA的度数为时，四边形BPDO是菱形.
答案解析收藏纠错 + 选题
19. (2019·夏津模拟) 如图，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A，C，E在同一直线上．
1. （1）求斜坡CD的高度DE；
2. （2）求大楼AB的高度（结果保留根号）
答案解析收藏纠错 + 选题
20. (2024七下·东莞期中) 某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元。
1. （1）求购买一个足球、一个篮球各需多少元？
2. （2）根据学校实际情况，需从体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？
答案解析收藏纠错 + 选题
21. (2019·河南模拟) 根据下列要求，解答相关问题：
1. （1）请补全以下求不等式﹣2x²﹣4x≥0的解集的过程
  ①构造函数，画出图象：
  
  根据不等式特征构造二次函数y=﹣2x²﹣4x；抛物线的对称轴x=﹣1，开口向下，顶点（﹣1，2）与x轴的交点是（0，0），（﹣2，0），用三点法画出二次函数y=﹣2x²﹣4x的图象如图1所示；
  
  ②数形结合，求得界点：
  
  当y=0时，求得方程﹣2x²﹣4x=0的解为；
  
  ③借助图象，写出解集：
  
  由图象可得不等式﹣2x²﹣4x≥0的解集为．
2. （2）利用（1）中求不等式解集的方法步骤，求不等式x²﹣2x+1＜4的解集．
  ①构造函数，画出图象；
  
  ②数形结合，求得界点；
  
  ③借助图象，写出解集．
3. （3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式ax²+bx+c＞0（a＞0）的解集．
答案解析收藏纠错 + 选题
22. (2019·河南模拟)
1. （1）问题发现：
  如图1，在正方形ABCD中，点E、F分别是边BC、AB上的点，且CE=BF，连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC，请判断：FG与CE的数量关系是，位置关系是．
2. （2）拓展探究：
  如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请出判断判断予以证明；
3. （3）类比延伸：
  如图3，若点E、F分别是BC、AB延长线上的点，其它条件不变，（1）中结论是否仍然成立？请直接写出你的判断．
答案解析收藏纠错 + 选题
23. (2019·河南模拟) 如图，二次函数y=ax²+bx+c的图象与x轴的交点为A、D（A在D的右侧），与y轴的交点为C，且A（4，0），C（0，﹣3），对称轴是直线x=1．
1. （1）求二次函数的解析式；
2. （2）若M是第四象限抛物线上一动点，且横坐标为m，设四边形OCMA的面积为s．请写出s与m之间的函数关系式，并求出当m为何值时，四边形OCMA的面积最大；
3. （3）设点B是x轴上的点，P是抛物线上的点，是否存在点P，使得以A，B、C，P四点为顶点的四边形为平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题