四川省成都市2019届九年级数学中考模拟试卷

更新时间：2019-05-20 浏览次数：515 类型：中考模拟

一、单选题

1. (2019·成都模拟) 在实数0，﹣ $\text{[math]}$ ， $\text{[math]}$ ，﹣2中，最小的是（）

A . ﹣2 B . ﹣ $\text{[math]}$ C . 0 D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·成都模拟) 在函数y= $\text{[math]}$ 中，自变量x的取值范围是（）

A . x＞ $\text{[math]}$ B . x≤ $\text{[math]}$ C . x≠ $\text{[math]}$ D . x≥ $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019·成都模拟) 四川省是全国重要的蔬菜主产区、“南菜北运”和冬春蔬菜优势区，位于成都市彭州濛阳镇的四川省农产品交易中心，日交量超过5000吨，年交易额超过150亿元，是省内设施最先进，交易量最大的蔬菜专业批发市场，也是全国第二大蔬菜产地交易中心。已初步形成了“西部第一、全国一流”绿色蔬菜产业和“农工贸一体化、产加销一条龙”的发展新格局。其中150亿元，用科学记数法表示为（）

A . 1.5×10²元 B . 1.5×10¹¹元 C . 1.5×10¹⁰元 D . 15×10⁹元

答案解析收藏纠错 + 选题
4. (2019·成都模拟) 一个几何体的三种视图如图所示，则这个几何体是（）

A . 长方体 B . 圆锥 C . 圆台 D . 圆柱

答案解析收藏纠错 + 选题
5. (2024八上·深圳期末) 若点A（1+m，1﹣n）与点B（﹣3，2）关于y轴对称，则m+n的值是（）

A . ﹣5 B . ﹣3 C . 3 D . 1

答案解析收藏纠错 + 选题
6. (2020·广东模拟) 如图，在△ABC中，D，E分别是AB，AC边上的点，DE∥BC，∠ADE=35°，∠C=120°，则∠A为（）

A . 60° B . 45° C . 35° D . 25°

答案解析收藏纠错 + 选题
7. (2019·成都模拟) 分式方程 $\text{[math]}$ 的解为（）

A . x=1 B . x=2 C . 无解 D . x=4

答案解析收藏纠错 + 选题
8. (2019·成都模拟) 如图，正方形ABCD内接于⊙O，AB=2 $\text{[math]}$ ，则 $\text{[math]}$ 的长是（）

A . π B . $\text{[math]}$ π C . 2π D . $\text{[math]}$ π

答案解析收藏纠错 + 选题
9. (2019·成都模拟) 如图所示，▱ABCD中，EF过对角线的交点O，如果AB=6cm，AD=5cm，OF=2cm，那么四边形BCEF的周长为（）

A . 13cm B . 15cm C . 11cm D . 9.5cm

答案解析收藏纠错 + 选题
10. (2019·成都模拟) 如图，二次函数y＝x²﹣2x﹣3的图象与x轴交于A、B两点，与y轴交于点C，则下列说法错误的是（）

A . AB＝4 B . ∠ABC＝45° C . 当x＞0时，y＜﹣3 D . 当x＞1时，y随x的增大而增大

答案解析收藏纠错 + 选题

二、解答题

11. (2019·成都模拟) 分解因式3x³﹣12x²y+12xy²=.

答案解析收藏纠错 + 选题
12. (2019·成都模拟)
1. （1）计算：|﹣ $\text{[math]}$ |+ $\text{[math]}$ ﹣4sin45°﹣ $\text{[math]}$ ．
2. （2）解不等式组 $\text{[math]}$ ，并把它的解集在如下的数轴上表示出来．
答案解析收藏纠错 + 选题
13. (2019·成都模拟) 如图，我国海监船在钓鱼岛附近的O处观测到一可疑船正匀速直线航行我国海域，当该可疑船位于点O的北偏东30°方向上的点A处（OA=20 $\text{[math]}$ km）时，我方开始向对方喊话，但该可疑船仍匀速航行，40min后，又测得该可疑船位于点O的正北方向上的点B处，且OB=20km，求该可疑船航行的速度．

答案解析收藏纠错 + 选题
14. (2019·成都模拟) 先化简，再求值： $\text{[math]}$ ，其中a= $\text{[math]}$ ﹣2．

答案解析收藏纠错 + 选题
15. (2019·成都模拟) 如图是一间摄影展览厅，其东、西面各有一个入口A、B，南面为出口C，北面分别有两个出口D、E，摄影爱好者郑浩任选一个入口进入展览厅，参观结束后，任选一个出口离开。
1. （1）郑浩从进入到离开共有多少种可能的结果？请画出树形图；
2. （2）求出郑浩从入口A进入展览厅并从北面出口离开的概率。
答案解析收藏纠错 + 选题
16. (2019·成都模拟) 如图，直线y=﹣x+2与反比例函数y= $\text{[math]}$ （k≠0）的图象交于A（a，3），B（3，b）两点，过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D．
1. （1）求a，b的值及反比例函数的解析式；
2. （2）若点P在直线y=﹣x+2上，且S_△_ACP=S_△_BDP ，请求出此时点P的坐标；
3. （3）在x轴正半轴上是否存在点M，使得△MAB为等腰三角形？若存在，请直接写出M点的坐标；若不存在，说明理由．
答案解析收藏纠错 + 选题
17. (2019·成都模拟) 如图1，D是⊙O的直径BC上的一点，过D作DE⊥BC交⊙O于E、N，F是⊙O上的一点，过F的直线分别与CB、DE的延长线相交于A、P，连结CF交PD于M，∠C＝ $\text{[math]}$ ∠P．
1. （1）求证：PA是⊙O的切线；
2. （2）若∠A＝30°，⊙O的半径为4，DM＝1，求PM的长；
3. （3）如图2，在（2）的条件下，连结BF、BM；在线段DN上有一点H，并且以H、D、C为顶点的三角形与△BFM相似，求DH的长度．
答案解析收藏纠错 + 选题
18. (2019·成都模拟) 在茶节期间，某茶商订购了甲种茶叶90吨，乙种茶叶80吨，准备用A、B两种型号的货车共20辆运往外地．已知A型货车每辆运费为0.4万元，B型货车每辆运费为0.6万元．
1. （1）设A型货车安排x辆，总运费为y万元，写出y与x的函数关系式；
2. （2）若一辆A型货车可装甲种茶叶6吨，乙种茶叶2吨；一辆B型货车可装甲种茶叶3吨，乙种茶叶7吨．按此要求安排A、B两种型号货车一次性运完这批茶叶，共有哪几种运输方案？
3. （3）说明哪种方案运费最少？最少运费是多少万元？
答案解析收藏纠错 + 选题
19. (2019·成都模拟) 阅读下面材料：
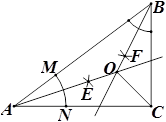
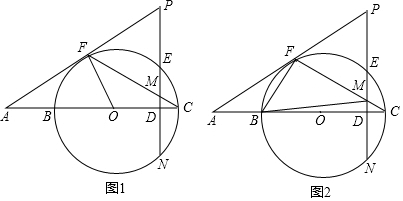
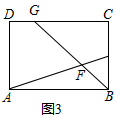
小明遇到这样一个问题：如图1，在正方形ABCD中，点E是边BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若AB=6，AF=4EF，求CG的值与∠AFB的度数．

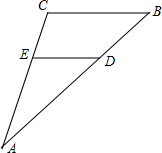
他的做法是：过点E作EH∥AB交BG于点H，得到△BAF∽△HEF（如图2）．
1. （1） CG等于多少，∠AFB等于多少度；
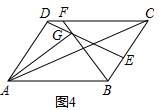
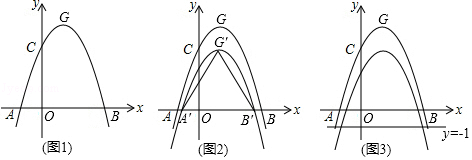
  参考小明思考问题的方法，解决下列问题；
2. （2）如图3，在矩形ABCD中，点E是边BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若AF=3EF，求 $\text{[math]}$ 的值；
3. （3）如图4，在平行四边形ABCD中，E、F分别是边BC、CD上的点，BF和DE相交于点G，且AB=kAD，∠DAG=∠BAC，求出 $\text{[math]}$ 的值（用含k的式子表示）
答案解析收藏纠错 + 选题
20. (2019·成都模拟) 如图1，抛物线C₁：y=ax²﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C₁的顶点为G．
1. （1）求出抛物线C₁的解析式，并写出点G的坐标；
2. （2）如图2，将抛物线C₁向下平移k（k＞0）个单位，得到抛物线C₂ ，设C₂与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：
3. （3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C₁、C₂于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．
答案解析收藏纠错 + 选题

三、填空题

21. (2019·成都模拟) 某课外小组调查了20户家庭某月的用电量，如下表所示

用电量（千瓦时）

120

140

160

180

200

户数

2

3

6

7

2

则这20户家庭该月用电量的平均数是（千瓦时），中位数是（千瓦时）．

答案解析收藏纠错 + 选题
22. (2019·成都模拟) 已知反比例函数y＝ $\text{[math]}$ ，当x≥3时，则y的取值范围是．

答案解析收藏纠错 + 选题
23. (2022·济宁模拟) 如图，在△ABC中，AB＝5，AC＝4，BC＝3，按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB、AC于点M、N；②分别以点M、N为圆心，以大于 $\text{[math]}$ 的长为半径作弧，两弧相交于点E；③作射线AE；④以同样的方法作射线BF，AE交BF于点O，连接OC，则OC＝.

答案解析收藏纠错 + 选题
24. (2019·成都模拟) 已知a，b为一元二次方程x²+2x﹣9=0的两个根，那么a²+a﹣b的值为．

答案解析收藏纠错 + 选题
25. (2019·成都模拟) 在一个不透明的盒子里装有4个分别写有数字﹣2，﹣1，0，1，2的小球，它们除数字不同外其余全部相同，现从盒子里随机取出一个小球，将该小球上的数字为m，点P的坐标为（m，m²+1），则点P落在抛物线y=﹣4x²+8x+5与x轴所围成的区域内（含边界）的概率是．

答案解析收藏纠错 + 选题
26. (2019·成都模拟) 如图，E是矩形ABCD边AD上一点，以DE为直径向矩形内部作半圆O，AB=4 $\text{[math]}$ ，OD=2，点G在矩形内部，且∠GCB=30°，GC=2 $\text{[math]}$ ，过半圆弧（含点D，E）上动点P作PF⊥AB于点F．当△PFG是等边三角形时，PF的长是．

答案解析收藏纠错 + 选题
27. (2019·成都模拟) 如图，双曲线y= $\text{[math]}$ （x＜0）经过Rt△ABC的两个顶点A，C，∠ABC=90°，AB∥x轴，连接OA，将Rt△ABC沿AC翻折后得到Rt△AB′C，点B′刚好落在线段OA上，连接OC，OC恰好平分OA与x轴负半轴的夹角，若Rt△ABC的面积为2，则k的值为．

答案解析收藏纠错 + 选题
28. (2019·成都模拟) 如图，在△ABC中，∠B=45°，AB=10，BC=8，DE是△ABC的中位线．过点D、E作DF∥EG，分别交BC于F、G，沿DF将△BDF剪下，并顺时针旋转180°与△AMD重叠，沿EG将△CEG剪下，并逆时针旋转180°与△ANE重叠，则四边形MFGN周长的最小值是．

答案解析收藏纠错 + 选题