广东省深圳市2019届高三第一次（2月)调研考试数学理试题

更新时间：2024-07-13 浏览次数：319 类型：高考模拟

一、单选题

1. (2019·深圳模拟) 复数 $\text{[math]}$ 的共轭复数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019高一下·成都月考) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2019·深圳模拟) 设 $\text{[math]}$ 为等差数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的公差为（）

A . -2 B . -1 C . 1 D . 2

答案解析收藏纠错 + 选题
4. (2019高一下·佛山月考) 已知某产品的销售额 $\text{[math]}$ 与广告费用 $\text{[math]}$ 之间的关系如下表：

$\text{[math]}$ （单位：万元）

0

1

2

3

4

$\text{[math]}$ （单位：万元）

10

15

20

30

35

若求得其线性回归方程为 $\text{[math]}$ ，则预计当广告费用为6万元时的销售额为（）

A . 42万元 B . 45万元 C . 48万元 D . 51万元

答案解析收藏纠错 + 选题
5. (2019·深圳模拟) 如图所示，网格纸上小正方形的边长为1，粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为（）

A . 72 B . 64 C . 48 D . 32

答案解析收藏纠错 + 选题
6. (2019高一下·成都月考) 已知直线 $\text{[math]}$ 是函数 $\text{[math]}$ 与的图象的一条对称轴，为了得到函数 $\text{[math]}$ 的图象，可把函数 $\text{[math]}$ 的图象（）

A . 向左平行移动 $\text{[math]}$ 个单位长度 B . 向右平行移动 $\text{[math]}$ 个单位长度 C . 向左平行移动 $\text{[math]}$ 个单位长度 D . 向右平行移动 $\text{[math]}$ 个单位长度

答案解析收藏纠错 + 选题
7. (2019·深圳模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，则 $\text{[math]}$ （）

A . -2 B . -1 C . 0 D . 1

答案解析收藏纠错 + 选题
8. (2019·深圳模拟) 古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论，利用尺规作图可画出已知线段的黄金分割点，具体方法如下：（l）取线段 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线，并用圆规在垂线上截取 $\text{[math]}$ ，连接 $\text{[math]}$ ；（2）以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ；（3）以 $\text{[math]}$ 为圆心，以 $\text{[math]}$ 为半径画弧，交 $\text{[math]}$ 于点 $\text{[math]}$ ．则点 $\text{[math]}$ 即为线段 $\text{[math]}$ 的黄金分割点．若在线段 $\text{[math]}$ 上随机取一点F，则使得 $\text{[math]}$ 的概率约为（）（参考数据： $\text{[math]}$ ）

A . 0.236 B . 0.382 C . 0.472 D . 0.618

答案解析收藏纠错 + 选题
9. (2019·深圳模拟) 已知偶函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，且当 $\text{[math]}$ 时，不等式 $\text{[math]}$ 恒成立，则使得 $\text{[math]}$ 成立的 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020·梅河口模拟) 已知直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ 两点，以 $\text{[math]}$ 为直径的圆恰好经过双曲线的右焦点 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则双曲线的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2019·深圳模拟) 已知 $\text{[math]}$ 为球 $\text{[math]}$ 的球面上的三个定点， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为球 $\text{[math]}$ 的球面上的动点，记三棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ ，三棱锥 $\text{[math]}$ 的体积为 $\text{[math]}$ ，若 $\text{[math]}$ 的最大值为3，则球 $\text{[math]}$ 的表面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2019高二下·柳州期中) 若关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 有正整数解，则实数 $\text{[math]}$ 的最小值为（）

A . 6 B . 7 C . 8 D . 9

答案解析收藏纠错 + 选题

二、填空题

13. (2019·深圳模拟) 设 $\text{[math]}$ 满足约束条件 $\text{[math]}$ ，则目标函数 $\text{[math]}$ 的最大值为．

答案解析收藏纠错 + 选题
14. (2019高三上·广东月考) 若 $\text{[math]}$ 的展开式中各项系数之和为32，则展开式中 $\text{[math]}$ 的系数为．

答案解析收藏纠错 + 选题
15. (2020·河南模拟) 已知点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，点 $\text{[math]}$ 是抛物线 $\text{[math]}$ 的焦点，直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点，若点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，且 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题

16. (2019·深圳模拟) 如图，在平面四边形 $\text{[math]}$ 中， $\text{[math]}$ 与 $\text{[math]}$ 为其对角线，已知 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 平分 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
17. (2019·深圳模拟) 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 是边长为1的菱形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 为 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，且 $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若平面 $\text{[math]}$ 底面 $\text{[math]}$ ，且 $\text{[math]}$ ，求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 所成锐二面角的余弦值．
答案解析收藏纠错 + 选题
18. (2019高二下·广州期中) 在平面直角坐标系 $\text{[math]}$ 中，椭圆 $\text{[math]}$ 的中心在坐标原点 $\text{[math]}$ ，其右焦点为 $\text{[math]}$ ，且点 $\text{[math]}$ 在椭圆 $\text{[math]}$ 上．
1. （1）求椭圆 $\text{[math]}$ 的方程；
2. （2）设椭圆的左、右顶点分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 是椭圆上异于 $\text{[math]}$ ， $\text{[math]}$ 的任意一点，直线 $\text{[math]}$ 交椭圆 $\text{[math]}$ 于另一点 $\text{[math]}$ ，直线 $\text{[math]}$ 交直线 $\text{[math]}$ 于 $\text{[math]}$ 点，求证： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点在同一条直线上．
答案解析收藏纠错 + 选题
19. (2019·深圳模拟) 某健身机构统计了去年该机构所有消费者的消费金额（单位：元），如下图所示：
1. （1）将去年的消费金额超过 3200 元的消费者称为“健身达人”，现从所有“健身达人”中随机抽取 2 人，求至少有 1 位消费者，其去年的消费金额超过 4000 元的概率；
2. （2）针对这些消费者，该健身机构今年欲实施入会制，详情如下表：
  
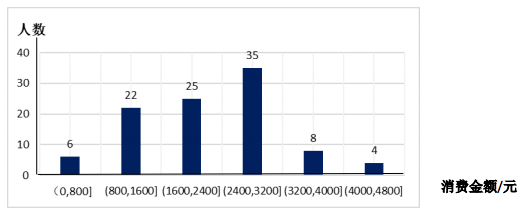
  会员等级
  
  消费金额
  
  普通会员
  
  2000
  
  银卡会员
  
  2700
  
  金卡会员
  
  3200
  
  预计去年消费金额在 $\text{[math]}$ 内的消费者今年都将会申请办理普通会员，消费金额在 $\text{[math]}$ 内的消费者都将会申请办理银卡会员，消费金额在 $\text{[math]}$ 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时，需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动，现有如下两种预设方案：
  
  方案 1：按分层抽样从普通会员，银卡会员，金卡会员中总共抽取 25 位“幸运之星”给予奖励：普通会员中的“幸运之星”每人奖励 500 元；银卡会员中的“幸运之星”每人奖励 600 元；金卡会员中的“幸运之星”每人奖励 800 元.
  
  方案 2：每位会员均可参加摸奖游戏，游戏规则如下：从-个装有 3 个白球、 2 个红球（球只有颜色不同）的箱子中，有放回地摸三次球，每次只能摸-个球.若摸到红球的总数消费金额/元为 2，则可获得 200 元奖励金；若摸到红球的总数为 3，则可获得 300 元奖励金；其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏；每位银卡会员均可参加 2 次摸奖游戏；每位金卡会员均可参加 3 次摸奖游戏（每次摸奖的结果相互独立） .
  
  以方案 2 的奖励金的数学期望为依据，请你预测哪-种方案投资较少？并说明理由.
答案解析收藏纠错 + 选题
20. (2019·深圳模拟) 已知函数 $\text{[math]}$ ，其定义域为 $\text{[math]}$ .（其中常数 $\text{[math]}$ ，是自然对数的底数）
1. （1）求函数 $\text{[math]}$ 的递增区间；
2. （2）若函数 $\text{[math]}$ 为定义域上的增函数，且 $\text{[math]}$ ，证明： $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2019·深圳模拟) 选修 4－4：坐标系与参数方程：在直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 的参数方程为 $\text{[math]}$ （ $\text{[math]}$ 为参数），以坐标原点为极点， $\text{[math]}$ 轴的正半轴为极轴建立极坐标系，曲线 $\text{[math]}$ 的极坐标方程为 $\text{[math]}$ ，直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 交于不同的两点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求曲线 $\text{[math]}$ 的参数方程；
2. （2）若点 $\text{[math]}$ 为直线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
22. (2019·深圳模拟) 选修 4－5：不等式选讲：设函数 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求不等式 $\text{[math]}$ 的解集；
2. （2）若不等式 $\text{[math]}$ 在 $\text{[math]}$ 上恒成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题