一、选择题(本大题共16个小题,共42分.1~10小题各3分,11~16小题各2分.)
-
-
2.
(2019·海港模拟)
把一个数写成ax10
n(1≤a<10,n为整数)的形式为3.57×10
-5 , 则原数为( )
A . 0.0000357
B . 0.000357
C . 357000
D . 3570000
-
-
-
5.
(2019·海港模拟)
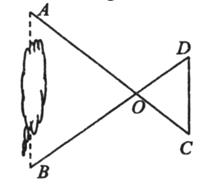
如图,A、B两地之间有一池塘,要测量A、B两地之间的距离,选择一点O,连接AO并延长到点C,使OC=

AO,连接BO并延长到点D,使OD=

BO.测得C、D间距离为30米,则A、B两地之间的距离为( )
A . 30米
B . 45米
C . 60米
D . 90米
-
A .  =±2
B . 2+
=±2
B . 2+  =2
=2  C . a2·a4=a8
D . (a3)2=a6
C . a2·a4=a8
D . (a3)2=a6
-
-
A . 1
B . -1
C . 2
D . -2
-
9.
(2019·海港模拟)
甲、乙、丙、丁四名射击运动员参加了预选赛,他们的射击成绩的平均环数

及方差
s2见下表所示:
| | 甲 | 乙 | 丙 | 丁 |
|  | 8 | 9 | 9 | 8 |
| s2 | 1 | 1 | 1.2 | 1.3 |
从中选一位平均成绩好且成绩稳定的选手参加比赛,应该选( )
A . 甲
B . 乙
C . 丙
D . 丁
-
-
A . 对角线相等的四边形是平行四边形
B . 有一个角是直角的四边形是矩形
C . 有一组邻边相等的平行四边形是菱形
D . 对角线互相垂直平分的四边形是正方形
-
12.
(2019·海港模拟)
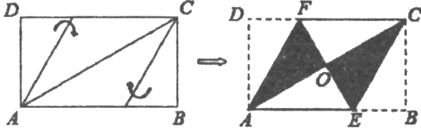
如图,将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AD=

, 则菱形AECF的面积为( )
-
13.
(2021七上·英德月考)
甲、乙、丙三人玩一种游戏,每玩一局都会将三人随机分成两组.积分方法举例说明:第一局甲、乙胜出,分别获得3分,丙获得-6分;第二局甲胜出获得12分,乙、丙分别获得-6分,两局之后的积分是:甲15分,乙3分,丙-12分.下表是三人的逐局积分统计表,计分错误开始于( )
| | 甲 | 乙 | 丙 |
| 第一局 | 3 | 3 | -6 |
| 第二局 | 15 | -3 | -12 |
| 第三局 | 21 | 3 | -24 |
| 第四局 | 15 | -3 | -12 |
| 第五局 | 12 | -6 | -6 |
| 第六局 | 0 | 18 | 12 |
A . 第三局
B . 第四局
C . 第五局
D . 第六局
-
-
15.
(2019·海港模拟)
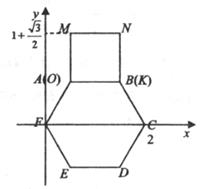
已知正方形MNKO和正六边形ABCDEF边长均为1,把正方形放在正六边形外边,使OK边与AB边重合,如图所示.按下列步骤操作:
将正方形在正六边形外绕点B顺时针旋转,使KN边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使NM边与CD边重合,完成第二次旋转;...在这样连续6次旋转的过程中,点M在图中直角坐标系中的纵坐标可能是( )
A . 2.2
B . -2.2
C . 2.3
D . -2.3
二、填空题(本大题有3个小题,共12分.17-18小题各3分,19小题6分.)
-
-
17.
(2019·海港模拟)
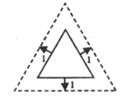
用一根长为a(cm)的铁丝,首尾相接围成一个等边三角形。要将它按如图的方式向外等距扩1(cm),得到新的等边三角形,则新的等边三角形的周长是
cm。
-
18.
(2019·海港模拟)
已知A、B两地之间的距离为20千米,甲步行,乙骑车,两人沿着相同路线由A地到B地匀速前行,甲、乙行进的路程S(千米)与x(小时)的函数图象如图所示。

-
-
(2)
在整个运动过程中,甲、乙两人之间的距离随x的增大而增大时,x的取值范围是 。
三、解答题(本大题共7个小题,共66分,解答应写出文字说明、证明过程或演算步骤)
-
19.
(2019·海港模拟)
定义新运算:对于任意数a,b,都有a0b=(a-b)(a
2+ab+b
2)+b
3 , 等式右边是通常的加法、减法、乘法及乘方运算,比如:5⊕2=(5-2)×(5
2+5×2+2
2)+2
3=3×39+8=117+8=125
-
-
(2)
化简(a-b)(a2+ab+b2)+b3 .
-
20.
(2019·海港模拟)
某学生会倡导的“爱心捐款活动结束后,学生会干部对捐款情况作了抽样调查,并绘制了统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人。
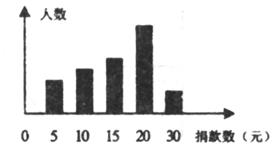
-
-
-
(3)
若该校共有2310名学生,请估算有多少人捐款数不少于20元?
-
21.
(2019·海港模拟)
如图,△MBC和△DBE均为等腰直角三角形.∠ABC=∠DBE=90°
求证:AD=CE;AD⊥CE.

-
22.
(2019·海港模拟)
如图,在平面直角坐标系中,□ABCD,顶点A(1,b),B(3,b),D(2,b+1)
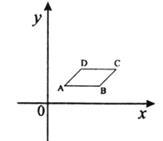
-
-
(2)
双曲线y=

,过□ABCD的顶点B和D,求该双曲线的表达式
-
(3)
如果□ABCD与双曲线y=

(x>0)总有公共点,求b的取值范围.
-
23.
(2019·海港模拟)
发现如图,在有一个“凹角∠A
1A
2A
3”的n边形A
1A
2A
3A
4…A
n中(n为大于3的整数),
∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+.....+∠An-(n-4)×180°
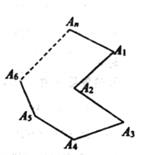
-
(1)
验证:如图
 ,
,
在有一个“凹角∠ABC”的四边形ABCD中,
证明:∠ABC=∠A+∠C+∠D
-
(2)
如图
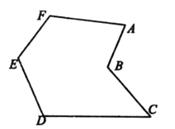 ,
,
在有一个“凹角∠ABC”的六边形ABCDEF中,
证明:∠ABC=∠A+∠C+∠D+∠E+∠F-360°
-
(3)
延伸:如图
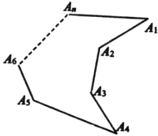 ,
,
在有两个连续“凹角∠A1A2A3的和∠A2A3A4”的n边形A1A2A3A4……..An(n为大于4的整数),
∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6 . ...…+∠An-(n- )×180
-
24.
(2019·海港模拟)
某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m(件)与时间t(天)的关系如下表:
|
时间t(天)
|
1
|
3
|
5
|
7
|
…
|
|
日销售量m(件)
|
94
|
90
|
86
|
82
|
…
|
未来40天内,前20天每天的价格y1(元/件)与时间t(天)的函数关系式为y1=0.25+25(1≤t≤20,且t为整数),后20天每天的价格y2=-0.5t+40(21≤t≤40,且t为整数),下面我们来研究销售这种商品的有关问题。
-
(1)
认真分析上表中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据的m(件)与t(天)之间的关系式;
-
(2)
请预测未来40天中哪一天的日销售利润最大,最大日销售利润是多少?
-
(3)
在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润,(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
-
25.
(2019·海港模拟)
如图,半圆D的直径AB=4,线段OA=7,O为原点,点B在数轴的正半轴上运动,点B在数轴上所表示的数为m.
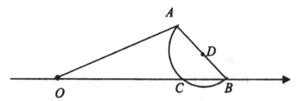
-
-
(2)
半圆D与数轴有两个公共点,设另一个公共点为C.
①直接写出m的取值范围是.
-
(3)
当△A0B的内心、外心与某一个顶点在同一条直线上时,求tan∠AOB的值。

 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 






 ,
, ,
, ,
,