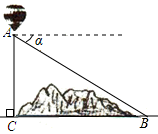
B .
B .  C .
C .  D .
D . 


方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
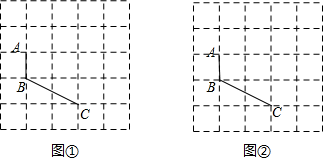
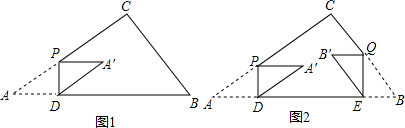
要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.
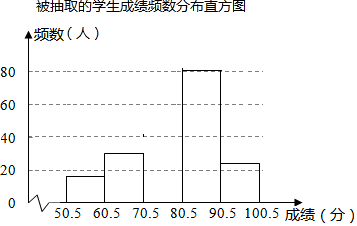
| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5~60.5 | 16 | 0.08 |
| 二 | 60.5~70.5 | 40 | 0.20 |
| 三 | 70.5~80.5 | 50 | 0.25 |
| 四 | 80.5~90.5 | m | 0.35 |
| 五 | 90.5~100.5 | 24 | n |
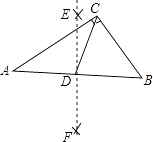
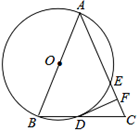
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是 .(只填结果)