
 B .
B .  C .
C .  D .
D . 


![]()

收集数据:现随机抽取七年级中40名同学“趣味数学知识竞赛”的成绩,如下(单位:分):
7585758075758570759075808070758085808095
9575908070809585758580807080758080557060
整理分析:小彬按照如下表格整理了这组数据,并绘制了如下的频数直方图。

问题解决:


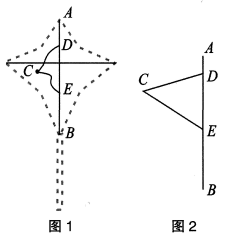
数学活动:在综合与实践活动课上,老师让同学们以“三角形纸片的折叠、旋转”为主题开展数学活动,探究线段长度的有关问题.
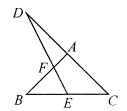
动手操作:如图1,在直角三角形纸片ABC中,∠BAC=90°,AB=6,AC=8.将三角形纸片ABC进行以下操作:
第一步:折叠三角形纸片ABC使点C与点A重合,然后展开铺平,得到折痕DE;
第二步:将△ABC沿折痕DE展开,然后将△DEC绕点D逆时针方向旋转得到△DFG,点E,C的对应点分别是点F,G,射线GF与边AC交于点M(点M不与点A重合),与边AB交于点N,线段DG与边AC交于点P.
数学思考:

问题解决:
①如图2,当GF∥BC时,求AM的长;
②如图3,当GF经过点B时,AM的长为
③当△DEC绕点D旋转至DE平分∠FDG的位置时,试在图4中作出此时的△DFG和射线GF,并直接写出AM的长(要求:尺规作图,不写作法,保留作图痕迹,标记出所有相应的字母)
如图,抛物线y=-x2-2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C.点D(m,0)为线段OA上一个动点(与点A,O不重合),过点D作x轴的垂线与线段AC交于点P,与抛物线交于点Q,连接BP,与y轴交于点E.

①是否存在一点D,使得PQ+ PC取得最大值?若存在,求此时m的值;若不存在,请说明理由;
②连接CQ,当线段PE=CQ时,直接写出m的值.