称图形的是( )
 B .
B .  C .
C .  D .
D . 
如图,是由一个圆柱体和一个长方体组成的几何体.其主视图是( )
 B .
B .  C .
C . 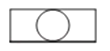 D .
D . 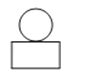






①计第:-14+15x[(- )
(-
)]-(32
23)÷(-7)
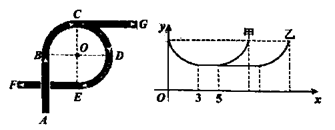
②若x,y在数轴上的位置如图所示,
![]()
化简:[(x2-y) (x2+y)]+[(x+y)
(x-y)]
|
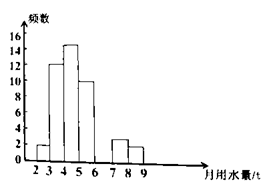
月均用水量(单位:t) |
频数 |
百分比 |
|
2≤x<3 |
2 |
4% |
|
3≤x<4 |
12 |
24% |
|
4≤x<5 |
||
|
5≤x<6 |
10 |
20% |
|
6≤x<7 |
12% |
|
|
7≤x<8 |
3 |
6% |
|
8≤x<9 |
2 |
4% |
例如,y=3x+2的4分函数为:当x≤4时,y|4|=-3x+2;当x>4时,y|4|=-3x-2.
①当x=4时,求y|2|;②当y|2|=3时,求x

当0≤t≤20,y=;当20<t≤40时,y=;

